微分積分学・同演習B (2020年度)

2020年10月12日11:49作成

2021年2月2日09:59更新

授業の日時

水曜日3時限目
遠隔授業

教科書

この授業は次の教科書に沿って進めます。特に演習は教科書中の演習問題を中心に行います。

微分積分学講義
野村隆昭 著
共立出版

授業の進め方、演習について

今学期，少なくとも春学期期間は Moodle による遠隔授業を行います．

授業時間（13時〜14時30分）とその前後1時間に講義ノートと講義の音声ファイルを Moodle にアップします．講義ノートをダウンロードして，それを見ながら講義音声を聞くことで受講完了となります．
授業時間以降，土曜日まで Moodle に掲示される課題に解答し，解答をレポートにまとめたものを pdfスキャンして，Moodle コースに提出して下さい．締め切りは授業のあった週の金曜日までとします．

授業予定

これはあくまで予定であり，実際の授業内容は諸般の事情により変更になることがあります．

10月7日ユークリッド空間の距離と位相

1.0. ガイダンス

1.1. 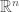$\mathbb{R}^n$ の復習

定義6.1. $\mathbb{R}^n$ の内積，ベクトルの直交関係，ノルム
Pythagorasの定理，補題6.3. Cauchy-Schwarz不等式，命題6.2. ノルムの公理

1.2. 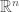$\mathbb{R}^n$ の位相

$\boldsymbol{x}\in \mathbb{R}^n$ の $\epsilon$ 近傍 $B_{\epsilon}(\boldsymbol{x})$
$S\subset \mathbb{R}^n$ の内点，外点，境界点，境界点の集合 $\partial S$ と閉包 $\bar{S}$
$\mathbb{R}^n$ の開集合，閉集合
$\mathbb{R}^n$ の曲線 (分) と連結部分集合，領域，閉領域

1.3. 関数の極限

$\displaystyle{ \lim_{\boldsymbol{x}\to\boldsymbol{0}}\,f(\boldsymbol{x})=c}$ の定義

10月14日偏微分と全微分

2.1. 連続関数と偏微分

2変数関数の連続性
領域 $S\subset \mathbb{R}^2$ 上の関数 $f :S\rightarrow \mathbb{R}$ の方向微分可能性と $\boldsymbol{v}$ 方向微分 $D_{\boldsymbol{v}}f(\boldsymbol{x})$ , 特に偏微分 $f_x(\boldsymbol{x})$ , $f_y(\boldsymbol{x})$

2.2. 全微分

領域 $S\subset \mathbb{R}^2$ 上の関数 $f :S\rightarrow \mathbb{R}$ の全微分可能性
領域 $S\subset \mathbb{R}^2$ 上の $C^1$ 級関数
定理6.19: $C^1$ 級関数は全微分可能
偏微分可能関数の勾配 (gradient) $\nabla f(\boldsymbol{x})$

10月21日出張のため休講

10月28日 Jacobi 行列と連鎖律

領域 $S\subset \mathbb{R}^{n}$ 上の偏微分可能写像
$\displaystyle \boldsymbol{f} : S\ni\boldsymbol{x} \longmapsto \begin{pmatrix} f_1(\boldsymbol{x}) \\ \vdots \\ f_m(\boldsymbol{x}) \end{pmatrix} \in \mathbb{R}^m$
の Jacobi 行列
$\displaystyle \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}=\frac{\partial (f_1,\dots,f_m)}{\partial(x_1,\dots,x_n)}:= \begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \dots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \dots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & & \vdots \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & \dots & \frac{\partial f_m}{\partial x_n} \end{pmatrix}$
連鎖律
$\displaystyle \frac{\partial (f_1(\boldsymbol{g}),\dots,f_\ell(\boldsymbol{g}))}{\partial(x_1,\dots,x_n)} =\frac{\partial (f_1(\boldsymbol{g}),\dots,f_\ell(\boldsymbol{g}))}{\partial(g_1,\dots,g_m)} \frac{\partial (g_1,\dots,g_m)}{\partial(x_1,\dots,x_n)}$

11月4日 Taylor の定理

4.1. 高階偏導関数

2回偏微分可能な関数 $f$ と2回偏導関数 $f_{xx},\,f_{xy},\,f_{yx},\,f_{yy}$
$C^r$ 級関数(定義6.30), 偏微分の可換性(定理6.31)

4.2. Taylorの定理

2変数関数の Taylor の定理6.51.
Taylor 多項式の一意性 (命題6.54)

11月11日二次形式と2変数関数の極値

5.1. 二次形式

（2変数）二次形式，正定値，負定値，不定値二次形式（定義6.61）
二次形式と対称行列との関係．Cholesky分解の応用．

5.2. 2変数関数の極値

極大値，極小値の定義6.56
命題6.58: 極値点の必要条件
Hesse行列の定義6.60とそれを用いたTaylorの定理の記述
2変数関数の極地の判定定理6.66

11月18日月曜日の授業を行う日

11月25日陰関数の定理

6.1. 陰関数の定理

陰関数定理6.73

6.2. 参考：高次元への拡張

高次元の陰関数定理6.83

12月2日条件付き極値問題

7.1. 曲線の特異点(6.11節)

${f(x,y)}$ ; ${C^{2}}$ 級関数． ${Z(f)=\{(x,y)\in\mathbb{R}^{2}\mid f(x,y)=0\}}$ の特異点
${\boldsymbol{a}=(a,b)\in Z(f)}$ : ${\nabla f(\boldsymbol{a})=\boldsymbol{0}}$ .
特異点の例
1. 孤立点 (isolated point).
2. 結節点 (node).
3. 尖点 (cusp).

7.2. 条件付き極値(6.12節)

定理6.94+ ${\alpha}$

12月9日矩形上の重積分

8.1. 矩形上の重積分

矩形とその分割
矩形上の有界関数の積分可能性と重積分
Darbouxの定理7.4とその応用
連続関数の積分可能性 (定理7.7)

8.2. 面積の定義

有界集合の特性関数と面積
面積確定集合の例

12月16日重積分と累次積分

9.1. 面積確定集合上の重積分

面積確定集合上の積分可能性と重積分
連続関数の積分可能性 (定理7.19)
定理7.20 重積分の基本性質：線形性，正値性，積分領域についての加法性．

9.2. 累次積分

縦線集合上の重積分は累次積分で計算できる (定理7.21)．

12月23日変数変換と広義重積分

10.1. 重積分の変数変換

Jacobi行列式と，重積分の変数変換公式 (定理7.34)
例：極座標

10.2. 広義重積分

有界でない面積確定集合
非有界な面積確定集合上の連続関数の広義積分可能性と広義重積分
近似増加列による，広義積分可能性の判定法と広義重積分の計算法 (定理7.56)
例7.59：二次元正規分布の計算と，正規分布への応用

1月6日微分方程式とは

11.1. 微分方程式への導入

$n$ 階常微分方程式とその解，初期条件と初期値問題
正規形 (normal form) 微分方程式と，その一般解，特殊解，特異解
解法11.4. 自励系の微分方程式

11.2. 1階微分方程式の求積法

解法11.5. 変数分離形の微分方程式
解法11.6. 同次形の微分方程式

1月13日月曜日の授業を行う日

1月20日線形微分方程式

12.1. 1階線形微分方程式

定義12.1. 線形微分方程式と斉次線形微分方程式
解法12.2. 1階線形微分方程式の解法
応用例：Bernoulli微分方程式とRiccati微分方程式

12.2. 2階斉次線形微分方程式

補題12.6. Wronski行列式による解空間の基底の判定．
解法12.7. 行列の指数関数と2階斉次線形方程式の解．
命題12.8. 2階斉次線形方程式の一般解．

1月27日非斉次線形微分方程式

13.0. 連絡事項

次回，授業アンケートを行う．
次回，微分方程式と広義重積分についての確認証テストを実施する．

13.1. 定数変化法

定理13.1. 2階非斉次線形微分方程式に付随する斉次線形方程式の解が1つ与えられたとき，その方程式の解空間の基底と，非斉次線形方程式の一般解を求める方法．

13.2. 定数係数の場合

解法13.2. 右辺が多項式のとき
解法13.3. 右辺が指数関数のとき
解法13.4. 右辺が指数関数と多項式の積のとき

2月3日まとめ小テスト

成績評価について

成績はレポート課題、小テストの結果を総合的に判断して行います。