微分積分学・同演習B (2019)

2019年9月19日11:26作成
2020年2月12日19:31更新

授業の日時、場所

月曜日1時限目
2103教室

教科書

この授業は次の教科書に沿って進めます。特に演習は教科書中の演習問題を中心に行います。

微分積分学講義
野村隆昭 著
共立出版

授業の進め方、演習について

毎回授業の最初に演習をします。
1. 前回の授業のときにそれぞれの演習問題の解答者を指名しておきます。指名された人は授業時間が始まるまでに黒板に解答を書いておいてください。教科書の巻末にある解答を写すのではなく、自分の理解を反映して自身の言葉で書いてください。それが自分のためにもクラスメートのためにも大切です。
2. 黒板の解答に沿って、理解すべき点や解答で書くべきことを私が説明します。なるべくきちんとした解答が黒板に残るように朱筆を加えますが、説明の方もよく聞いてください。
3. なお、再履修の方は学期半ばまで履修者名簿に名前がないため、こちらから指名するのは難しいかもしれません。積極的に自分から名乗り出て演習を解くようにしてください。
続いて講義を行います。講義では
1. 基本的な概念 (定義) の説明。
2. それらの概念の満たす性質 (命題、定理など)。
3. それらの性質を使って計算する方法 (例題) の解説。
についてお話しします。ときどき命題や定理の証明もしますが、それは内容をよりよく理解して使えるようになってもらうためで、証明を覚える必要は特にありません。
最後に次回の演習の解答者を決めます。基本的にはこちらで指名します。演習では主に教科書の問や章末問題を解いてもらいます。
いうまでもなく数学は自分で考えて練習問題を解くことで理解していく科目です。毎回の練習問題は解答者だけでなく履修者全員の宿題です。1時間やそこらで解ける量ですから、必ず授業があったその日のうちに解いて、習った内容を理解しておきましょう。一人では解けないときには皆で相談し、助け合って問題を解くことも大切な演習の目的です。

授業内容

以下はあくまでも予定であり，諸般の事情により変更になることがあります．

10月7日 $\mathbb{R}^{n}$ の距離，連続関数

$\mathbb{R}^{n}=\{(x_{1},\dots,x_{n})\mid x_{i}\in\mathbb{R}\}$ の内積

$\boldsymbol{x}\cdot\boldsymbol{y}:=\sum_{i=1}^{n}\,x_{i}y_{i}\in\mathbb{R}$
とノルム $\|\boldsymbol{x}\|:=\sqrt{\boldsymbol{x}\cdot\boldsymbol{x}}=\sqrt{\sum_{i=1}^{n}\,x_{i}^{2}}\geqq0$
$\boldsymbol{x}\bot \boldsymbol{y}$ $\Leftrightarrow$ $\boldsymbol{x}\cdot\boldsymbol{y}=0$ .
Pythagorasの定理： $\boldsymbol{x}\bot \boldsymbol{y}\in\mathbb{R}^{n}$ のとき， $\|\boldsymbol{x}+\boldsymbol{y}\|^{2}=\|\boldsymbol{x}\|^{2}+\|\boldsymbol{y}\|^{2}.$
Cauchy-Schwarzの不等式 (補題6.3): $|\boldsymbol{x}\cdot\boldsymbol{y}|\leqq \|\boldsymbol{x}\|\|\boldsymbol{y}\|$
命題6.2: $\|\ \|$ はノルムの公理を満たす．特に三角不等式が大事．

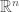$\mathbb{R}^n$ の位相

部分集合 $S\subset\mathbb{R}^{n}$ の内点，外点，境界点，境界点の集合 $\partial S$ と閉包 $\bar{S}=S\cup \partial S$
$\mathbb{R}^n$ の開および閉部分集合
$S\subset\mathbb{R}^{n}$ 内の曲線 $C: [0,1]\ni t\mapsto \boldsymbol{p}(t)\in S$
$S$ が連結とは， $\forall \boldsymbol{x}$ , $\boldsymbol{y}\in S$ ,
$\exists C:[0,1]\ni t\mapsto\boldsymbol{p}(t)\in S$ ; 曲線 s.t. $\boldsymbol{p}(0)=\boldsymbol{x}$ ,
$\boldsymbol{p}(1)=\boldsymbol{y}$ となること．

関数 $f:S\rightarrow\mathbb{R}$ が $\boldsymbol{a}\in\bar{S}$ で $\alpha\in \mathbb{R}$ に収束: $\displaystyle \lim_{\boldsymbol{x}\to\boldsymbol{a}}\,f(\boldsymbol{x})=\alpha$
$\Longleftrightarrow$
$\forall\varepsilon>0$ , $\exists\delta>0$ s.t. $|f(\boldsymbol{x})-\alpha|<\varepsilon$ , ( $\forall\boldsymbol{x}\in S$ , $|\boldsymbol{x}-\boldsymbol{a}|<\delta$ ).

演習問題

問題1 ${S=\{(x,y)\in\mathbb{R}^{2}\mid0<x<1,\,0<y<1\}}$ は開集合であることを示せ．

問題2 ${D:=\{(x,y)\in\mathbb{R}^{2}\mid x^{2}+y^{2}\leqq1\}}$ は閉集合であることを示せ．

問題3 ${X:=\{(x,y)\in\mathbb{R}^{2}\mid x>0,\,y\geqq0\}}$ は開集合でも閉集合でもないことを示せ．

問題4 次の ${\mathbb{R}^{2}}$ の部分集合の境界点の集合を求めよ．
(1)問題2の ${D}$ .
(2)問題3の ${X}$ .

問題5 教科書p.125の問題6.6.

10月14日体育の日

10月16日（水曜日！）偏微分と全微分

2.1. 偏微分

定義6.7 ${f:S\rightarrow\mathbb{R}}$ が ${\boldsymbol{a}\in S}$ で連続
${{\displaystyle \Longleftrightarrow\quad \lim_{\boldsymbol{x}\rightarrow\boldsymbol{a}}\,f(\boldsymbol{x})=f(\boldsymbol{a})}}$ ．

定義 ${S\subset\mathbb{R}^{2}}$ ；開集合， ${f:S\rightarrow\mathbb{R}}$ ; 関数， ${(x,y)\in S}$ .
${(u,v)\not=0}$ に対して，方向微分

$\displaystyle D_{(u,v)}f(x,y):=\lim_{t\rightarrow0}\frac{f(x+ut,y+vt)-f(x,y)}{t}$

が存在するとき， ${f}$ は ${(x,y)}$ で ${(u,v)}$ 方向微分可能という．
特に

$\displaystyle f_{x}(x,y)=\frac{\partial f}{\partial x}(x,y):=D_{(1,0)}f(x,y),$

$\displaystyle f_{y}(x,y)=\frac{\partial f}{\partial y}(x,y):=D_{(0,1)}f(x,y)$

を ${f}$ の ${(x,y)}$ での ${x}$ についての(resp. ${y}$ についての) 偏微分という．

2.2. 全微分

定義6.15. ${f:S\rightarrow\mathbb{R}}$ が ${\boldsymbol{a}=(a,b)\in S}$ で全微分可能
${\Longleftrightarrow}$ ${\exists(p,q)\in \mathbb{R}^{2}}$ s.t.

$\displaystyle f(a+tu,b+tv)=f(a,b)+t(p,q)\cdot (u,v)+o(t),\quad\forall(u,v)\not=(0,0),\,\in\mathbb{R}^{2}.$

${\Longleftrightarrow}$ ${\exists(p,q)\in \mathbb{R}^{2}}$ s.t. ${D_{(u,v)}f(a,b)=(p,q)\cdot(u,v)}$ , ${\forall(u,v)\not=(0,0),\,\in\mathbb{R}^{2}}$ .
このとき ${f_{x}(a,b)=p}$ , ${f_{y}(a,b)=q}$ ．

定義6.18. ${f:S\rightarrow\mathbb{R}}$ が ${\boldsymbol{a}=(a,b)\in S}$ で ${C^{1}}$ 級
${\Longleftrightarrow}$ ${f}$ は ${\boldsymbol{a}}$ で偏微分可能で， ${f_{x}}$ , ${f_{y}}$ は ${\boldsymbol{a}}$ で連続．

定理6.19. ${C^{1}}$ 級なら全微分可能．

2.3. 演習問題
問題6.9, 6.20, 6.27.

10月21日 Jacobi 行列と連鎖律

3.1. Jacobi行列(6.6節)

偏微分可能な関数 ${f_{1},\dots,f_{m}:S\rightarrow\mathbb{R}}$ が与える写像
$\displaystyle \boldsymbol{f}=(f_{1},\dots, f_{m}): S \longrightarrow \mathbb{R}^{m}$

のJacobi行列

$\displaystyle \frac{\partial(f_{1},\dots,f_{m})}{\partial(x_{1},\dots,x_{n})}(\boldsymbol{x}) =\begin{pmatrix}\dfrac{\partial f_{1}}{\partial x_{1}}(\boldsymbol{x}) & \dfrac{\partial f_{1}}{\partial x_{2}}(\boldsymbol{x}) & \dots & \dfrac{\partial f_{1}}{\partial x_{n}}(\boldsymbol{x})\\ \dfrac{\partial f_{2}}{\partial x_{1}}(\boldsymbol{x}) & \dfrac{\partial f_{2}}{\partial x_{2}}(\boldsymbol{x}) & \dots & \dfrac{\partial f_{2}}{\partial x_{n}}(\boldsymbol{x})\\ \vdots & \vdots & \ddots & \vdots\\ \dfrac{\partial f_{m}}{\partial x_{1}}(\boldsymbol{x}) & \dfrac{\partial f_{m}}{\partial x_{2}}(\boldsymbol{x}) & \dots & \dfrac{\partial f_{m}}{\partial x_{n}}(\boldsymbol{x}) \end{pmatrix}\in\mathbb{M}_{m,n}(\mathbb{R}).$

定理6.34 ${S\subset\mathbb{R}^{n}}$ , ${T\subset\mathbb{R}^{m}}$ ; 開集合． ${g_{1},\dots,g_{m}:S\rightarrow\mathbb{R}}$ , ${f_{1},\dots,f_{\ell}:T\rightarrow\mathbb{R}}$ ; ${C^{1}}$ 級関数，が ${\boldsymbol{g}(S)\subset T}$ を満たすとき，

$\displaystyle \frac{\partial(f_{1}(\boldsymbol{g}), \dots, f_{\ell}(\boldsymbol{g}))}{\partial(x_{1},\dots,x_{n})} =\frac{\partial(f_{1}(\boldsymbol{g}),\dots,f_{\ell}(\boldsymbol{g}))}{\partial(g_{1},\dots,g_{m})} \frac{\partial(g_{1},\dots,g_{m})}{\partial(x_{1},\dots,x_{n})}.$

例：極座標 ${x=r\cos\theta}$ , ${y=r\sin\theta}$ , ( ${r\geq0}$ , ${0\leqq\theta<2\pi}$ ).

3.2. 演習問題

問題3.1. ${f(x(t),y(t))}$ の ${t}$ についての微分を求めよ．
(1) ${f(x,y)=x^{2}-y^{2}}$ , ${x(t)=t^{2}+1}$ , ${y(t)=2t}$ .

(2) ${f(x,y)=\dfrac{x-y}{x+y}}$ , ${x(t)=t}$ , ${y(t)=\dfrac{1}{t}}$ .

(3) ${f(x,y)=x^{2}y^{2}-x^{2}y^{4}}$ , ${x(t)=\cos t}$ , ${y(t)=\sin t}$ .

(4) ${f(x,y)=\log\dfrac{y}{x}}$ , ${x(t)=\cosh t}$ , ${y(t)=\sinh t}$ .

問題3.2. ${f(x,y)}$ , ${g(x,y)}$ に対するJacobi行列 ${{\displaystyle \frac{\partial(f,g)}{\partial(x,y)}}}$ を求めよ．

$\displaystyle \text{(1) }f(x,y)=x^{p}y^{q}, g(x,y)=x^{q}y^{p},\qquad\text{(2) }f(x,y)=x\cos^{n}y, g(x,y)=x\sin^{n}y$

$\displaystyle \text{(3) }f(x,y)=\log(x\log y), g(x,y)=y\log(\log x),$

$\displaystyle \text{(4) }f(x,y)=\cosh x\cos y, g(x,y)=\sinh x\sin y$

10月28日 Taylor の定理

4.1. 高階偏導関数(6.4節)

小テスト．
${f_{xy}=(f_{x})_{y}=\dfrac{\partial}{\partial y}\dfrac{\partial f}{\partial x}=\dfrac{\partial^{2}f}{\partial y\partial x}}$ , ${f_{xyx}=\dfrac{\partial^{3}f}{\partial x\partial y\partial x}}$ などと書く．
${C^{r}}$ 級関数， ${C^{\infty}}$ 級関数の定義．

定理6.31. ${S\subset\mathbb{R}^{2}}$ ; 開部分集合．関数 ${f:S\rightarrow\mathbb{R}}$ が ${C^{2}}$ 級なら ${f_{xy}=f_{yx}}$ ．

4.2. Taylorの定理

Taylorの定理6.51. ${f(x,y)}$ が ${C^{n+1}}$ 級関数のとき，ある ${0<\theta<1}$ に対して

$\displaystyle f(x+a,y+b)= \sum_{k=0}^{n}\sum_{j=0}^{k}\,\frac{1}{k!}\begin{pmatrix} k \\ j \end{pmatrix} \frac{\partial^{k}f(x,y)}{\partial x^{j}\partial y^{k-j}}a^{j}b^{k-j}$

$\displaystyle +\sum_{j=0}^{n+1}\,\frac{1}{(n+1)!} \begin{pmatrix} n+1 \\ j \end{pmatrix} \frac{\partial^{n+1}f(x+a\theta,y+b\theta)}{\partial x^{j}\partial y^{n-j+1}}a^{j}b^{n-j+1}.$

4.3. 演習問題

教科書の問題6.28, 37, 38, 39, 41.

問題4.1. 次の関数の ${(0,0)}$ の周りでのTaylor展開を3次の項まで求めよ．

$\displaystyle \text{(1) }\cos(x+y)\quad\text{(2) }e^{x+y}\log(1+x)$

11月4日文化の日振替休日

11月11日二次形式

5.1. 二次形式

2変数二次形式 ${Q(x,y)=ax^{2}+2bxy+dy^{2}=\begin{pmatrix} x & y\end{pmatrix}\begin{pmatrix}a & b\\ b & d \end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}}$ . この行列 ${S=\begin{pmatrix}a & b\\ b & d \end{pmatrix}}$ の性質によって挙動が決まる．

スペクトル定理　(i) ${S=\begin{pmatrix}a & b\\ b & d \end{pmatrix}}$ の特性多項式 ${\det(xE-S)=x^{2}-(a+d)x+ad-b^{2}}$ は実根 ${\alpha}$ , ${\beta\in\mathbb{R}}$ を持つ．
(ii)直交行列 ${T}$ (i.e. ${T^{-1}={}^{t}T}$ )があって

$\displaystyle T^{-1}ST={}^{t}TST=\begin{pmatrix} \alpha & 0 \\ 0 & \beta \end{pmatrix}.$

5.2. 二次形式の極値

命題　2変数二次形式 ${Q(x,y)=ax^{2}+2bxy+dy^{2}=\begin{pmatrix} x & y\end{pmatrix}\begin{pmatrix}a & b\\ b & d \end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}}$ について

正定値: $ad-b^2>0$ かつ $a+d>0$ ( ${\alpha,}$ ${\beta>0}$ )のとき， ${Q(x,y)}$ は ${(0,0)}$ で極小値．
負定値: $ad-b^2>0$ かつ $a+d<0$ ( ${\alpha}$ , ${\beta<0}$ )のとき， ${Q(x,y)}$ は ${(0,0)}$ で極大値．
不定値: $ad-b^2<0$ ( ${\alpha\beta<0}$ )のとき， ${(0,0)}$ は ${Q(x,y)}$ の鞍点．

5.3. 演習問題

問題5.1. ${S=\begin{pmatrix} 1 & 2\\ 2 & 3 \end{pmatrix}}$ の直交対角化を求めよ．

11月18日陰関数の定理

小テスト
中間テストの連絡

6. 2変数関数の極値のための十分条件

命題6.58. ${f(x,y)}$ を ${C^{2}}$ 級関数とする． ${f}$ が ${(a,b)}$ で極値を取るならば， ${f_{x}(a,b)=f_{y}(a,b)=0}$ ．

${f}$ のHesse行列を ${H_{f}(x,y):=\begin{pmatrix}f_{xx}(x,y) & f_{xy}(x,y)\\ f_{xy}(x,y) & f_{yy}(x,y) \end{pmatrix}}$ と定義．

定理6.67. ${C^{2}}$ 級関数 ${f(x,y)}$ が ${f_{x}(a,b)=f_{y}(a,b)=0}$ を満たすとする．
(1) ${\det H_{f}(a,b)0}$ のとき，次の2つの可能性がある:

${\mathrm{tr} H_{f}(a,b)>0}$ なら ${f}$ は ${(a,b)}$ で極小値を取る．
${\mathrm{tr} H_{f}(a,b)<0}$ なら ${f}$ は ${(a,b)}$ で極大値を取る．

6.2. 陰関数

陰関数定理6.73. ${f(x,y)}$ ; ${C^{1}}$ 級関数， ${f(a,b)=0}$ かつ ${f_{y}(a,b)\not=0}$ とする．
(i) ${\exists r>0}$ , ${\exists\varphi:(a-r,a+r)\rightarrow\mathbb{R}}$ ; ${C^{1}}$ 級関数 s.t. ${\varphi(a)=b}$ かつ ${f(x,\varphi(x))=0}$ .

(ii)そのとき ${\varphi'(a)=-\dfrac{f_{x}(a,b)}{f_{y}(a,b)}}$ .

6.3. 演習問題
教科書p.150の問題6.71の(1), (3), (5), p.154の問題6.78.

11月25日条件付き極値

小テスト

7.1. 曲線の特異点(6.11節)

${f(x,y)}$ ; ${C^{2}}$ 級関数に対し， ${C(f)=\{(x,y)\in\mathbb{R}^{2}\mid f(x,y)=0\}}$ は曲線．
${\boldsymbol{a}=(a,b)\in Z(f)}$ が ${C(f)}$ の特異点 ${\Longleftrightarrow}$ ${\nabla f(\boldsymbol{a})=\boldsymbol{0}}$ .
復習： ${C(f)}$ の非特異点 ${\boldsymbol{a}}$ での接線の方程式は ${\nabla f(\boldsymbol{a})\cdot(\boldsymbol{x}-\boldsymbol{a})=0}$ .
特異点の例
1. ${H_{f}(\boldsymbol{a})}$ が非可逆(尖点，cusp).
2. ${H_{f}(\boldsymbol{a})}$ が不定値(結節点，node).
3. ${H_{f}(\boldsymbol{a})}$ が負定値(孤立点，isolated point).

7.2. 条件付き極値(6.12節)

${f(x,y)}$ , ${g(x,y)}$ ; ${C^{2}}$ 級関数． ${f}$ を ${C(g)}$ に制限したもの ${f|_{C(g)}}$ の極値を求めたい．

定理6.94+ ${\alpha}$ ${f(x,y)}$ , ${g(x,y)}$ を ${C^{2}}$ 級関数とする．
(i) ${f}$ の ${C(g)}$ への制限が， ${C(g)}$ の非特異点 ${\boldsymbol{a}=(a,b)}$ で極値を取る． ${\Longmapsto}$ ${\nabla f(\boldsymbol{a})=\alpha\nabla g(\boldsymbol{a})}$ , ( ${\exists\alpha\in\mathbb{R}}$ ).
(ii) (i)の条件に加えて

$\displaystyle (g_{y}(\boldsymbol{a}),-g_{x}(\boldsymbol{a}))H_{f-\alpha g}(\boldsymbol{a})\begin{pmatrix}g_{y}(\boldsymbol{a})\\ -g_{x}(\boldsymbol{a}) \end{pmatrix}$

が正(負)ならば， ${f|_{C(g)}}$ は ${\boldsymbol{a}}$ で極小値(極大値)を取る．

7.3. 演習問題

問題7.1. 次の ${f(x,y)=0}$ の陰関数 ${y=\varphi(x)}$ の極値を求めよ．
(1) ${f=x-y+\log xy}$ .
(2) ${f=2xy^{3}-x^{2}+y}$ .
(3) ${f=x^{3}+3x^{2}+y^{3}-2y}$ .

12月2日中間テスト

12月9日矩形上の重積分

9.1. 矩形上の重積分(7.1節)

${R=[a,b]\times[c,d]}$ ; 矩形．区間の分割
$\displaystyle \Delta_{x}=(a=a_{0}<a_{1}<\dots<a_{n}=b),$

$\displaystyle \Delta_{y}=(c=c_{2}<c_{1}<\dots<c_{m}=d)$

の直積 ${\Delta:=\Delta_{x}\times\Delta_{y}=\left(\Delta_{i,j}=[a_{i-1},a_{i}]\times[b_{j-1},b_{j}]\mid1\leqq i\leqq n,\,1\leqq j\leqq m\right)}$ を ${R}$ の分割という．

$\displaystyle |\Delta_{i,j}|:=(a_{i}-a_{i-1})(b_{j}-b_{j-1})$

$\displaystyle \ell(\Delta):=\max_{\substack{1\leqq i\leqq n \\ 1\leqq j\leqq m }}\, \ell(\Delta_{i,j}), \quad \ell(\Delta_{i,j}):=\max(a_{i}-a_{i-1},b_{j}-b_{j-1}).$
${f:R\rightarrow\mathbb{R}}$ ; 有界関数． ${\Delta}$ ; ${R}$ の分割， ${\boldsymbol{a}_{i,j}\in\Delta_{i,j}}$ , ( ${1\leqq i\leqq n}$ , ${1\leqq j\leqq m}$ ).
$\displaystyle R(f,\Delta;\{\boldsymbol{a}_{i,j}\}) :=\sum_{i=1}^{n}\sum_{j=1}^{m}\,f(\boldsymbol{a}_{i,j})\cdot|\Delta_{i,j}|,$

$\displaystyle S(f,\Delta):=\sum_{i=1}^{n}\sum_{j=1}^{m}\,\sup_{\boldsymbol{x}\in\Delta_{i,j}}\,f(\boldsymbol{x})\cdot|\Delta_{i,j}|,$

$\displaystyle s(f,\Delta):=\sum_{i=1}^{n}\sum_{j=1}^{m}\,\inf_{\boldsymbol{x}\in\Delta_{i,j}}\,f(\boldsymbol{x})\cdot|\Delta_{i,j}|.$

$\displaystyle \therefore\quad\inf_{\boldsymbol{x}\in R}\,f(\boldsymbol{x})\cdot|R|\leqq s(f,\Delta)\leqq R(f,\Delta;\{\boldsymbol{a}_{i,j}\})\leqq S(f,\Delta)\leqq\sup_{\boldsymbol{x}\in R}\,f(\boldsymbol{x})\cdot|R|.$

定義7.2. ${s(f):={\displaystyle \sup_{\Delta}\,s(f,\Delta)}}$ , ${{\displaystyle S(f):=\inf_{\Delta}\,S(f,\Delta)}}$ が一致するとき， ${f}$ は ${R}$ 上で積分可能，その値を

$\displaystyle \iint_{R}\,f(x,y)\,dxdy$

と書く．

Darbouxの定理7.4. ${f}$ が ${R}$ 上で積分可能ならば

$\displaystyle \lim_{\ell(\Delta)\rightarrow0}\,s(f,\Delta) =\lim_{\ell(\Delta)\rightarrow0}\,S(f,\Delta)=\iint_{R}\,f(x,y)\,dxdy.$

特に

$\displaystyle \lim_{\ell(\Delta)\rightarrow0}\,R(f,\Delta,\{\boldsymbol{a}_{i,j}\})=\iint_{R}\,f(x,y)\,dxdy.$

定理7.7. ${f:R\rightarrow\mathbb{R}}$ が連続なら ${f}$ は ${R}$ 上で積分可能．

9.2. 面積の定義(7.2節)

${D\subset\mathbb{R}^{2}}$ ; 部分集合の特性関数 (characteristic function):
$\displaystyle \chi_{D}(x,y):=\begin{cases} 1 & (x,y)\in D;\\ 0 & (x,y)\notin D. \end{cases}$

定義7.12. ${D\subset\mathbb{R}^{2}}$ ; 有界集合． ${\exists R=[a,b]\times[c,d]}$ s.t. ${D\subset R}$ .
${\chi_{D}}$ が ${R}$ 上で積分可能なとき:

$\displaystyle \sup_{\Delta}\,\sum_{\Delta_{i,j}\subset D}\,|\Delta_{i,j}|=\inf_{\Delta}\,\sum_{\Delta_{i,j}\cap D\not=\varnothing}\,|\Delta_{i,j}|,$

${D}$ は面積確定 (measurable)であるといい，

$\displaystyle \mu(D):=\iint_{R}\,\chi_{D}(x,y)\,dxdy$

を ${D}$ の面積 (area)という．

境界が連続曲線であっても面積確定とは限らない(Jordan曲線など)．

9.3. 演習問題
教科書p.178の問題7.11 (1), (3), (5), p.181の問題7.16.

12月16日重積分と累次積分

10.1. 重積分(7.3節)

定義7.17. ${D\subset\mathbb{R}^{2}}$ ; 面積確定集合． ${f:\mathbb{R}^{2}\rightarrow\mathbb{R}}$ ; 有界関数．
${f}$ が ${D}$ 上で積分可能 (integrable)
${\Longleftrightarrow}$
${\exists R\supset D}$ ; 矩形 s.t. ${\chi_{D}f}$ は ${R}$ 上で積分可能．そのとき

$\displaystyle \iint_{D}\,f(x,y)\,dxdy:=\iint_{R}\,f(x,y)\chi_{D}(x,y)\,dxdy$

と書く．

定理7.19. ${D\subset\mathbb{R}^{2}}$ ; 面積確定， ${f}$ ; 連続関数 ${\Mapsto}$ ${f}$ は ${D}$ 上で積分可能．

定理7.20 (重積分の基本性質). ${D}$ ; 面積確定閉集合， ${f}$ , ${g:D\rightarrow\mathbb{R}}$ ; 連続
(1)線形性：

$\displaystyle \iint_{D}\,(f+cg)(x,y)\,dxdy=\iint_{D}\,f(x,y)\,dxdy+c\iint_{D}\,g(x,y)\,dxdy,\quad c\in\mathbb{R}.$

(2)正値性：

$\displaystyle f(\boldsymbol{x})\geqq0,\quad\boldsymbol{x}\in D\quad\Longmapsto\quad\iint_{D}\,f(x,y)\,dxdy\geqq0.$

(3)加法性： ${D=D_{1}\cup D_{2}}$ かつ ${\mu(D_{1}\cap D_{2})=0}$ のとき

$\displaystyle \iint_{D}\,f(x,y)\,dxdy=\iint_{D_{1}}\,f(x,y)\,dxdy+\iint_{D_{2}}\,f(x,y)\,dxdy.$

10.2. 累次積分

定理7.21. 連続関数 ${\varphi}$ , ${\psi:[a,b]\rightarrow\mathbb{R}}$ が ${\varphi(x)\leqq\psi(x)}$ , ( ${a\leqq x\leqq b}$ )を満たすとき，

$\displaystyle D=\left\{ (x,y)\in\mathbb{R}^{2}\left|\begin{array}{c} a\leqq x\leqq b\\ \varphi(x)\leqq y\leqq\psi(x) \end{array}\right.\right\}$

を縦線集合 (ordinate set)という．任意の連続関数 ${f:D\rightarrow\mathbb{R}}$ は ${D}$ 上で積分可能で，

$\displaystyle \iint_{D}\,f(x,y)\,dxdy=\int_{a}^{b}\left(\int_{\varphi(x)}^{\psi(x)}\,f(x,y)\,dy\right)\,dx$

10.3. 演習問題
教科書p.187の問題7.25, p.188の問題7.27.

12月23日変数変換と広義重積分

極限の順序交換(7.6節)

累次積分の順番を交換すると計算が楽になることがある．

11.1. 重積分の変数変換

定理7.34. ${D\subset\mathbb{R}^{2}}$ ; 面積確定(有界閉)集合． ${C^{1}}$ 級全単射

$\displaystyle \boldsymbol{x}:D\ni(s,t)\longmapsto(x(s,t),y(s,t))\in E$

が ${\det\dfrac{\partial(x,y)}{\partial(s,t)}\not=0}$ , ${\forall(s,t)\in D}$ を満たすとき
(1) ${E}$ は面積確定．
(2) ${\forall f:E\rightarrow\mathbb{R}}$ ；連続関数

$\displaystyle \iint_{E}\,f(x,y)\,dxdy=\iint_{D}\,f(x(s,t),y(s,t)) \left|\det\frac{\partial(x,y)}{\partial(s,t)}\right|\,dsdt.$

例：2次元曲座標

11.2. 広義重積分

${D\subset\mathbb{R}^{2}}$ ; 集合が面積確定 (measurable)
${\Longleftrightarrow}$
${\forall K\subset\mathbb{R}^{2}}$ ; 面積確定有界閉集合， ${D\cap K}$ は面積確定．

定義7.52, 7.66. ${D\subset\mathbb{R}^{2}}$ ; 面積確定， ${f:D\rightarrow\mathbb{R}}$ ；連続関数．

$\displaystyle f_{+}(x,y):=\max(0,f(x,y)),\quad f_{-}(x,y):=\max(0,-f(x,y)).$

(i) ${f}$ が ${D}$ で(絶対)広義積分可能
${\Longleftrightarrow}$

${\displaystyle{ \mathcal{I}_{D}(f_{\pm}) := \bigg\{ \iint_{D\cap K}\, f_{\pm}(x,y)\,dxdy\,\bigg|\, K\subset\mathbb{R}^{2}}}$ 面積確定有界閉集合 $\displaystyle{\bigg\}}$ が上に有界．

(ii)そのとき

$\displaystyle {\displaystyle \iint_{D}\,f(x,y)\,dxdy}:=\sup\,\mathcal{I}_{D}(f_{+})-\sup\,\mathcal{I}_{D}(f_{-})$

を ${f}$ の ${D}$ 上の広義積分という．

; 面積確定集合の近似増加列とは，
1. 有界閉部分集合の増加列 ${D_{1}\subset D_{2}\subset\dots\subset D}$ で
2. ${\forall K\subset D}$ ; 面積確定有界閉集合， ${\exists n\in\mathbb{N}}$ s.t. ${K\subset D_{n}}$ を満たすもの．

定理7.56. ${\exists\{D_{n}\}}$ ; ${D}$ の近似増加列 s.t.

$\displaystyle \lim_{n\rightarrow\infty}\,\iint_{D_{n}}\,|f(x,y)|\,dxdy$

が存在すれば， ${f}$ は ${D}$ で広義積分可能で，

$\displaystyle \iint_{D}\,f(x,y)\,dxdy=\lim_{n\rightarrow\infty}\,\iint_{D_{n}}\,f(x,y)\,dxdy$

11.3. 演習問題
教科書p.189の問題7.30, p.193の問題7.36, p.194の問題7.41, p.203の問題7.61.

1月6日微分方程式とは

12.1. 微分方程式

${n}$ 階の（常）微分方程式 ((ordinary) differential equation)とその解．
初期条件 (initial condition)と初期値問題 (initial value problem)
正規形 (normal form)の微分方程式のみ扱う．
微分方程式の一般解 (general solution), 特殊解 (particular solution)，(2)の特異解 (singular solution)

12.2. 一階方程式の求積法

求積法 (quadrature)で解ける場合：
変数分離形 (separable)
同次形 (homogeneous)：変数分離形に帰着．

1月13日成人の日

1月14日（火曜日！）線形微分方程式

13.1. 一階線形微分方程式

線形微分方程式 (linear differential equation)
$\displaystyle a_{n}(x)y^{(n)}+a_{n-1}(x)y^{(n-1)}+\dots+a_{0}(x)y=b(x).$

さらに ${b(x)=0}$ のとき，同次 (homogeneous)であるという．
一階線形微分方程式
$\displaystyle y'+a(x)y=b(x)$

の解法．
Bernoulli方程式は一階線形微分方程式に帰着できる．
Riccati方程式の特殊解から一般解が構成できる．

13.2. 2階同次線形方程式

2階の同次線形微分方程式の解空間．その基底の Wronskian による判定法．
定数係数の同次線形微分方程式
$\displaystyle y''+py'+qy=0$

の解空間の基底の求め方．

1月20日非斉次線形微分方程式

授業アンケート

14.1. 定数変化法

定理14.1: 同次方程式

$\displaystyle y''+p(x)y'+q(x)y=0,\quad q(x)\not=0 \ \ \ \ \ (1)$

の解 ${u(x)}$ がわかっているとき，(!)の解空間の基底 ${\{u(x),v(x)\}}$ と，非同次方程式

$\displaystyle y''+p(x)y'+q(x)y=r(x)$

の一般解を求める方法．
定数係数のとき: ${D:=\dfrac{d}{dx}}$ のとき， ${(D^{2}+pD+q)y=r(x)}$ , ( ${p}$ , ${q\in\mathbb{R}}$ )の形の方程式は，形式的に ${y=\dfrac{r(x)}{D^{2}+pD+q}}$ を計算することで解けることがある．

1月27日出張のため休講

2月3日期末テスト

成績評価について

成績評価は中間、期末テストの結果および，授業中に提示するレポートの評点を総合的に判断して行います．

中間テスト

12月2日(月)の授業の時間に中間テストを行いました．

範囲：教科書の6章多変数関数の微分法
教科書，ノートなどの持ち込みは禁止．学生証と時計を持参すること．試験中の飲食は禁止します．
忌引，傷病などでやむを得ず欠席する場合は試験開始時刻までに基幹教育教務係まで連絡すること．

期末テスト

2月3日 (月) の授業の時間に期末テストを行いました．

2月12日（水）から基幹教育教務係で，期末テスト答案を返却してもらっています．履修者の皆さんは3月末日までに，各自の答案を受け取りに行ってください．

範囲は，教科書の7章多変数関数の積分法と，教科書には含まれていない微分方程式，12月9日から1月20日までの授業内容です．
教科書，ノートなどの持ち込みは禁止．学生証と時計を持参すること．試験中の飲食は禁止します．
忌引，傷病などでやむを得ず欠席する場合は試験開始時刻までに基幹教育教務係まで連絡すること．
中間テストを受験していない人は期末テストを受けることはできません．

今野拓也のページ

研究、教育関連の情報など

微分積分学・同演習B (2019)

授業の日時、場所

教科書

授業の進め方、演習について

授業内容

10月7日 $\mathbb{R}^{n}$ の距離，連続関数

$\mathbb{R}^{n}=\{(x_{1},\dots,x_{n})\mid x_{i}\in\mathbb{R}\}$ の内積

$\mathbb{R}^n$ の位相

演習問題

10月14日体育の日

10月16日（水曜日！）偏微分と全微分

10月21日 Jacobi 行列と連鎖律

10月28日 Taylor の定理

11月4日文化の日振替休日

11月11日二次形式

11月18日陰関数の定理

11月25日条件付き極値

12月2日中間テスト

12月9日矩形上の重積分

12月16日重積分と累次積分

12月23日変数変換と広義重積分

1月6日微分方程式とは

1月13日成人の日

1月14日（火曜日！）線形微分方程式

1月20日非斉次線形微分方程式

1月27日出張のため休講

2月3日期末テスト

成績評価について

中間テスト

期末テスト

授業の日時、場所

教科書

授業の進め方、演習について

授業内容

10月7日 の距離，連続関数

の内積

の位相

演習問題

10月14日 体育の日

10月16日（水曜日！）偏微分と全微分

10月21日 Jacobi 行列と連鎖律

10月28日 Taylor の定理

11月4日 文化の日振替休日

11月11日 二次形式

11月18日 陰関数の定理

11月25日 条件付き極値

12月2日 中間テスト

12月9日 矩形上の重積分

12月16日 重積分と累次積分

12月23日 変数変換と広義重積分

1月6日 微分方程式とは

1月13日 成人の日

1月14日（火曜日！）線形微分方程式

1月20日 非斉次線形微分方程式

1月27日 出張のため休講

2月3日 期末テスト

成績評価について

中間テスト

期末テスト

10月7日 $\mathbb{R}^{n}$ の距離，連続関数

$\mathbb{R}^{n}=\{(x_{1},\dots,x_{n})\mid x_{i}\in\mathbb{R}\}$ の内積

$\mathbb{R}^n$ の位相

10月14日体育の日

11月4日文化の日振替休日

11月11日二次形式

11月18日陰関数の定理

11月25日条件付き極値

12月2日中間テスト

12月9日矩形上の重積分

12月16日重積分と累次積分

12月23日変数変換と広義重積分

1月6日微分方程式とは

1月13日成人の日

1月20日非斉次線形微分方程式

1月27日出張のため休講

2月3日期末テスト