線形代数学・同演習A (2018年度)

2018年4月8日作成

2019年3月6日11:29最終更新

授業の日時，場所

水曜日2時限目
2204教室

教科書について

この授業では教科書は特に指定しません．演習問題などは毎回，板書またはプリントにして配布します．

授業の進め方

毎回授業の最初に演習をします．
1. 前回の授業のときにそれぞれの演習問題の解答者を指名しておきます．指名された人は授業時間が始まるまでに黒板に解答を書いておいてください．教科書の巻末にある解答を写すのではなく，自分の理解を反映して自身の言葉で書いてください．それが自分のためにもクラスメートのためにも大切です．
2. 黒板の解答に沿って，理解すべき点や解答で書くべきことを私が説明します．なるべくきちんとした解答が黒板に残るように朱筆を加えますが，説明の方もよく聞いてください．原則として，黒板に解答がない問題については解説しません．
3. なお、再履修の方は学期半ばまで履修者名簿に名前がないため，こちらから指名するのは難しいかもしれません．積極的に自分から名乗り出て演習を解くようにしてください．
続いて講義を行います．講義では
1. 基本的な概念 (定義) の説明
2. それらの概念の満たす性質 (命題、定理など)
3. それらの性質を使って計算する方法 (例題) の解説
についてお話しします．ときどき命題や定理の証明もしますが，それは内容をよりよく理解して使えるようになってもらうためで，証明を覚える必要は特にありません．
最後に次回の演習の解答者を指名します．

履修のコツ

線形代数に限らず数学科目では，前回まで学んだ内容の上に授業内容が積み重なって，複雑な概念を無理なく理解し，自分の考察に運用できるようにしていきます．喩えるならば，日々負荷を高めることで身体能力を上げていくアスリートの訓練のようなもので，このような能力を上げる目的には，日々の積み重ねが最も大切です．

そのためには，毎週の授業で学んだ内容をその日のうちに必ず復習し，出された演習問題を，これまた必ずその日のうちに解いてみることです．初回の授業からこの2点をきちんと実行していれば，学期末になって特に試験の準備をする必要はないはずです．逆に毎回の授業内容を習得することを怠っていれば，試験前にいくら詰め込み勉強をしたとしても，ほとんど効果はありません．簡単なことですので，履修者の皆さんは意志を持って上の2点を守るようにしてください．

授業予定

これはあくまで予定であり，事情により随時変更されることがあります．

4月11日掃き出しと線形方程式系

$m\times n$ 行列

$\displaystyle \begin{pmatrix}a_{1,1} & a_{1,2} & \dots & a_{1,n}\\ a_{2,1} & a_{2,2} & \dots & a_{2,n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m,1} & a_{m,2} & \dots & a_{m,n} \end{pmatrix}$

とその第 ${i}$ 行 (row) ${(a_{i,1},\dots,a_{i,n})}$ , 第 ${j}$ 列 (column) ${\begin{pmatrix}a_{1,j}\\ \vdots\\ a_{m,j} \end{pmatrix}}$ ．

${n}$ 次正方行列 (square matrix)，行ベクトル (row vector) と列ベクトル (column vector)．

Gauss-Jordan 消去法

行基本変形3種
階段行列 (rref)
1. 各行の ${0}$ でない最初の成分は ${1}$ .
2. そのような ${1}$ を含む列の他の成分は全て ${0}$ .
3. 下の行に行くほど最初の1は右に来る．
最初の1に対応する変数をそれ以外の (パラメーター) 変数で表す．

4月18日線型方程式系の解の構造

2.1. 連立一次方程式の解の構造
${m\times n}$ 行列 ${A=\begin{pmatrix}a_{1,1} & \dots & a_{1,n}\\ \vdots & \dots & \vdots\\ a_{m,1} & \dots & a_{m,n} \end{pmatrix}}$ ，列ベクトル ${\boldsymbol{b}=\begin{pmatrix}b_{1}\\ \vdots\\ b_{m} \end{pmatrix}}$ に対する連立一次方程式

$\displaystyle \left\{ \begin{array}{c} a_{1,1}x_{1}+\dots+a_{1,n}x_{n}=b_{1}\\ a_{2,1}x_{1}+\dots+a_{2,n}x_{n}=b_{2}\\ \vdots\\ a_{m,1}x_{1}+\dots+a_{m,n}x_{n}=b_{m} \end{array}\right. \ \ \ \ \ (1)$

命題2.1. (i) 一次方程式系(1)が解を持たないためには，簡約行列 ${\mathrm{rref}(A|\boldsymbol{b})}$ に ${(0\dots0|1)}$ の形の行があることが必要十分．

(ii) それ以外の場合，(1)がただ一つの解を持つためには， ${\mathrm{rref}(A)}$ の各列が，ある行の最初の1を含むことが必要十分．

定義2.1. 行列 ${A}$ の簡約行列 ${\mathrm{rref}(A)}$ の最初の1の個数を ${A}$ の階数 (rank)と呼んで ${\mathrm{rank}A}$ と書く．定義から ${\mathrm{rank}(A)\leqq\min(m,n)}$ ．

命題2.2. (i) ${\mathrm{rank}(A)=m}$ ならこの方程式系は解を持つ．

(ii) ${\mathrm{rank}(A)=n}$ ならこの方程式系は高々1つしか解を持たない．

(iii) ${\mathrm{rank}(A)<n}$ ならこの方程式系は無限個の解を持つか，解を持たないかのいずれかである．

系2.1. $n=m$ のとき，(1)がただ一つの解を持つためには， ${\mathrm{rref}(A)}$ が単位行列 (unit matrix)

$\displaystyle \begin{pmatrix}1 & 0 & \dots & 0\\ 0 & 1 & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \dots & 0 & 1 \end{pmatrix}$

であることが必要十分．

2.2. 一次方程式系のベクトル表示

定義2.2. ${m\times n}$ 行列 ${A=\left(\begin{array}{ccc} a_{1,1} & \dots & a_{1,n}\\ \vdots & \ddots & \vdots\\ a_{m,1} & \dots & a_{m,n} \end{array}\right)}$ , ${B=\left(\begin{array}{ccc} b_{1,1} & \dots & b_{1,n}\\ \vdots & \ddots & \vdots\\ b_{m,1} & \dots & b_{m,n} \end{array}\right)}$ と ${\boldsymbol{c}=\begin{pmatrix}c_{1}\\ c_{2}\\ \vdots\\ c_{n} \end{pmatrix}\in\mathbb{R}^{n}}$ に対して

$\displaystyle A+B:=\left(\begin{array}{ccc} a_{1,1}+b_{1,1} & \dots & a_{1,n}+b_{1,n}\\ \vdots & \ddots & \vdots\\ a_{m,1}+b_{m,1} & \dots & a_{m,n}+b_{m,n} \end{array}\right)$

$\displaystyle \lambda A:=\left(\begin{array}{ccc} \lambda a_{1,1} & \dots & \lambda a_{1,n}\\ \vdots & \ddots & \vdots\\ \lambda a_{m,1} & \dots & \lambda a_{m,n} \end{array}\right)$

$\displaystyle A\boldsymbol{c}=\begin{pmatrix}\boldsymbol{v}_{1} & \boldsymbol{v}_{2} & \dots & \boldsymbol{v}_{n}\end{pmatrix}\begin{pmatrix}c_{1}\\ c_{2}\\ \vdots\\ c_{n} \end{pmatrix}=c_{1}\boldsymbol{v}_{1}+c_{2}\boldsymbol{v}_{2}+\dots+c_{n}\boldsymbol{v}_{n}$

と書く．

$\displaystyle \boldsymbol{v}_{j}=\begin{pmatrix}a_{1,j}\\ a_{2,j}\\ \vdots\\ a_{m,j} \end{pmatrix},\quad(1\leqq j\leqq n),\qquad\boldsymbol{b}=\begin{pmatrix}b_{1}\\ b_{2}\\ \vdots\\ b_{m} \end{pmatrix}$

とおけば，上の方程式(1)は

$\displaystyle x_{1}\boldsymbol{v}_{1}+x_{2}\boldsymbol{v}_{2}+\dots+x_{n}\boldsymbol{v}_{n}=\boldsymbol{b}$

と書ける．これを一次方程式系のベクトル表示という．

定義2.3. 実数の集合を ${\mathbb{R}}$ と書き，実数係数の列ベクトル ${\begin{pmatrix}a_{1}\\ a_{2}\\ \vdots\\ a_{m} \end{pmatrix}}$ , ( ${a_{i}\in\mathbb{R}}$ )の集合を ${\mathbb{R}^{m}}$ で表す． ${\boldsymbol{b}\in\mathbb{R}^{m}}$ が ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{n}\in\mathbb{R}^{m}}$ の一次結合 (linear combination)であるとは，適当な ${c_{1},\dots,c_{n}\in\mathbb{R}}$ があって

$\displaystyle \boldsymbol{b}=c_{1}\boldsymbol{v}_{1}+c_{2}\boldsymbol{v}_{2}+\dots+c_{n}\boldsymbol{v}_{n}$

と表せることとする．

4月25日線形写像

3.1. 線形写像
集合 ${X}$ から集合 ${Y}$ への写像 (map) ${f:X\rightarrow Y}$ とは，各 ${x\in X}$ にただ1つの ${f(x)\in Y}$ を対応させるルールのこと．

定義3.1. 写像 ${f:\mathbb{R}^{n} \rightarrow \mathbb{R}^{m}}$ が線形写像 (linear map)であるとは，ある ${m\times n}$ 行列 ${A}$ があって

$\displaystyle f(\boldsymbol{x})=A\boldsymbol{x},\quad\boldsymbol{x}\in\mathbb{R}^{n}$

と書けること．

補題3.1. ${f:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}}$ を線形写像とするとき，

$\displaystyle f(\boldsymbol{x})=\begin{pmatrix}| & & |\\ f(\boldsymbol{e}_{1}) & \dots & f(\boldsymbol{e}_{n})\\ | & & | \end{pmatrix}\begin{pmatrix}x_{1}\\ x_{2}\\ \vdots\\ x_{n} \end{pmatrix}.$

命題3.1. 像 ${f:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}}$ が線形写像であるためには，任意の ${\boldsymbol{v}}$ , ${\boldsymbol{w}\in \mathbb{R}^{n}}$ , ${c\in\mathbb{R}}$ に対して

$\displaystyle f(\boldsymbol{v}+\boldsymbol{w})=f(\boldsymbol{v})+f(\boldsymbol{w}),\quad f(c\boldsymbol{v})=Ac\boldsymbol{v}=cA\boldsymbol{v}=cf(\boldsymbol{v})$

を満たすことが必要十分

3.2. 線形写像の例

例.1. (回転) ${\boldsymbol{x}\in\mathbb{R}^{2}}$ を反時計回りに ${\theta}$ 回転する写像 ${f :\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}}$ は行列 $\begin{pmatrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}$ に付随する線形写像．
例.2. 直線 ${\ell}$ : ${y=0}$ に沿っての剪断 (shear along ${\ell}$ ) ${f:\mathbb{R}^{2}\ni\boldsymbol{x}\mapsto\begin{pmatrix}1 & b\\ 0 & 1 \end{pmatrix}\boldsymbol{x}\in\mathbb{R}^{2}}$
例.3. (直交射影と鏡映) (i) ${\boldsymbol{v}\not=0}$ , ${\in\mathbb{R}^{2}}$ の張る直線 ${\ell}$ : ${\{c\boldsymbol{v}\mid c\in\mathbb{R}\}}$ への直交射影 (orthogonal projection):

$\displaystyle \mathrm{pr}_{\ell}:\mathbb{R}^{2}\ni\boldsymbol{x}\longmapsto\frac{\boldsymbol{x}\cdot\boldsymbol{v}}{\|\boldsymbol{v}\|^{2}}\boldsymbol{v}\in\mathbb{R}^{2}$

特徴付け:

$\displaystyle \mathrm{pr}_{\ell}(\boldsymbol{x})\in\ell,\quad(\boldsymbol{x}-\mathrm{pr}_{\ell}(\boldsymbol{x}))\bot\ell$

(ii) $\ell$ に関する鏡映 (reflection)

$\displaystyle \mathrm{ref}_{\ell}:\mathbb{R}^{2}\ni\boldsymbol{x}\longmapsto2\mathrm{pr}_{\ell}(\boldsymbol{x})-\boldsymbol{x}\in\mathbb{R}^{2}$

特徴付け:

$\displaystyle \frac{\boldsymbol{x}+\mathrm{ref}_{\ell}(\boldsymbol{x})}{2}\in\ell,\quad(\boldsymbol{x}-\mathrm{ref}_{\ell}(\boldsymbol{x}))\bot\ell$

5月2日金曜授業日

5月9日写像の合成と行列の積

4.1. 行列の積

写像 ${f:X\rightarrow Y}$ , ${g:Y\rightarrow Z}$ の合成 (composite)

$\displaystyle g\circ f:X\ni x\longmapsto g(f(x))\in Z$

命題4.1. (i) 線形写像

$\displaystyle f:\mathbb{R}^{n}\ni\boldsymbol{x}\longmapsto A\boldsymbol{x}\in\mathbb{R}^{m},\quad g:\mathbb{R}^{m}\ni\boldsymbol{y}\longmapsto B\boldsymbol{y}\in\mathbb{R}^{\ell}$

の合成 ${g\circ f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{\ell}}$ は再び線形写像．その( ${\ell\times n}$ )行列を ${B}$ と ${A}$ の積 (product)と呼び， ${BA}$ と書く．

(ii) ${A=(\boldsymbol{v}_{1},\boldsymbol{v}_{2},\dots,\boldsymbol{v}_{n})}$ と書くとき，

$\displaystyle BA=\begin{pmatrix} B\boldsymbol{v}_{1} & B\boldsymbol{v}_{2} & \dots & B\boldsymbol{v}_{n} \end{pmatrix}.$

4.2. 行列の積の性質

命題4.2. (i) ${m\times n}$ 行列 ${A}$ に対して， ${E_{m}A=AE_{n}=A}$ ．

(ii) ${\ell\times m}$ 行列 ${A}$ , ${B}$ , ${m\times n}$ 行列 ${C}$ , ${D}$ に対して，分配法則 ${(A+B)C=AC+BC}$ , ${A(C+D)=AC+AD}$ が成り立つ．

(iii) ${k\times\ell}$ 行列 ${A}$ , ${\ell\times m}$ 行列 ${B}$ , ${m\times n}$ 行列 ${C}$ に対して，結合法則 ${A(BC)=(AB)C}$ が成り立つ．

行列のブロック分け

5月16日可逆写像と逆行列

5.1. 線型変換の逆写像

定義5.1. 写像 ${f:X\rightarrow Y}$ が全単射 (bijection)または可逆 (invertible)
$\Longleftrightarrow$
任意の ${y\in Y}$ に対して ${f(x)=y}$ となる ${x\in X}$ がただ一つある.
このとき

$\displaystyle f^{-1}:Y\ni y\longmapsto(x;\, f(x)=y)\in X$

は写像．これを ${f}$ の逆写像 (inverse)という．

注意5.1. (i)写像 ${f:X\rightarrow Y}$ が全単射のとき， ${f^{-1}\circ f(x)=x}$ , ${f\circ f^{-1}(y)=y}$ , ( ${x\in X}$ , ${y\in Y}$ )が成り立つ．
(ii) ${f:X\rightarrow Y}$ が全単射のとき， ${(f^{-1})^{-1}=f}$ である．

定義5.2. ${m\times n}$ 行列 ${A}$ が可逆であるとは，線形写像 ${f: \mathbb{R}^{n} \ni \boldsymbol{v} \mapsto A\boldsymbol{v}\in\mathbb{R}^{m}}$ が可逆であること．

命題5.1. ${m\times n}$ 行列 ${A}$ が可逆であるためには，次の2条件が成り立つことが必要十分である．

${A}$ は正方行列である: ${m=n}$ .
${\mathrm{rref}(A)}$ は単位行列 ${E_{n}}$ に等しい．すなわち ${\mathrm{rank}(A)=n}$ である．

定義5.3. ${A}$ を可逆な ${n\times n}$ 行列とするとき，線形写像 ${f : \mathbb{R}^{n}\ni \boldsymbol{x}\mapsto A\boldsymbol{x}\in\mathbb{R}^{n}}$ の逆写像 ${f^{-1}:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n}}$ も線形写像.
その行列を ${A}$ の逆行列 (inverse matrix)と呼んで， ${A^{-1}}$ で表す．

命題5.2. ${A}$ を ${n}$ 次正方行列とする． ${A}$ が可逆であるためには， ${\mathrm{rref}(A|E_{n})}$ が ${(E_{n}|B)}$ の形であることが必要十分である．このとき ${A^{-1}=B}$ である．

5月23日線形写像の像と核

6.1. 線形写像の像

定義6.1. 写像 ${f:X\rightarrow Y}$ の像 (image)

$\displaystyle \mathrm{Im}\, f:=\{f(x)\mid x\in X\}$

定義6.2. ${\boldsymbol{v}_{1}, \dots, \boldsymbol{v}_{r} \in \mathbb{R}^{n}}$ の線形結合の集合

$\displaystyle \mathrm{span}\{\boldsymbol{v}_{1}, \dots, \boldsymbol{v}_{r}\}:=\{c_{1}\boldsymbol{v}_{1} +\dots+c_{r}\boldsymbol{v}_{r} \mid c_{1},\dots,c_{r}\in\mathbb{R}\}$

を ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}}$ で張られるまたは生成される空間 (span)という．

命題6.1. 線形写像 ${f:\mathbb{R}^{n}\ni\boldsymbol{v}\mapsto A\boldsymbol{v}\in\mathbb{R}^{m}}$ の行列を ${A=\left(\boldsymbol{v}_{1} \boldsymbol{v}_{2} \dots \boldsymbol{v}_{n} \right)}$ と書くとき，

$\displaystyle \mathrm{Im}\, f=\mathrm{span}\{\boldsymbol{v}_{1},\dots\boldsymbol{v}_{n}\}.$

これを ${A}$ の像ともいい， ${\mathrm{Im}\, A}$ と書く．

補題6.1. 線形写像 ${f:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}}$ の像は次の性質を持つ．

${0\in\mathrm{Im}\, f}$ .
${\boldsymbol{v},\,\boldsymbol{w}\in\mathrm{Im}\, f}$ ならば ${\boldsymbol{v}+\boldsymbol{w}\in\mathrm{Im}\, f}$ .
${\boldsymbol{v}\in\mathrm{Im}\, f}$ , ${c\in\mathbb{R}}$ に対して， ${c\boldsymbol{v}\in\mathrm{Im}\, f}$ .

6.2. 線形写像の核

定義6.3. 線形写像 ${f:\mathbb{R}^{n}\ni\boldsymbol{v}\mapsto A\boldsymbol{v}\in\mathbb{R}^{m}}$ , または ${A}$ の核 (kernel)

$\displaystyle \mathrm{Ker}\, f=\mathrm{Ker}\, A:=\{\boldsymbol{v}\in\mathbb{R}^{n}\mid f(\boldsymbol{v})=\mathbf{0}\}=\{\boldsymbol{v}\in\mathbb{R}^{n}\mid A\boldsymbol{v}=\boldsymbol{0}\}$

補題6.2. 線形写像 ${f:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}}$ の核は次の性質を持つ．

${0\in\mathrm{Ker}\, f}$ .
${\boldsymbol{v},\,\boldsymbol{w}\in\mathrm{Ker}\, f}$ ならば ${\boldsymbol{v}+\boldsymbol{w}\in\mathrm{Ker}\, f}$ .
${\boldsymbol{v}\in\mathrm{Ker}\, f}$ , ${c\in\mathbb{R}}$ に対して， ${c\boldsymbol{v}\in\mathrm{Ker}\, f}$ .

補題6.3. (i) ${m\times n}$ 行列 ${A}$ に対して， ${\mathrm{Ker}\, A=\{\boldsymbol{0}\}}$ であるためには ${\mathrm{rank}(A)=n}$ であることが必要十分である．

(ii)特に ${n}$ 次正方行列 ${A}$ が可逆であるためには， ${\mathrm{Ker}\, A=\{\mathbf{0}\}}$ であることが必要十分である．

5月30日前半の復習

6月6日中間テスト

6月13日 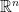${\mathbb{R}^{n}}$ の部分空間とその基底

7.1. 部分空間

定義7.1. 部分集合 ${V\subset\mathbb{R}^{n}}$ が部分空間 (subspace)
$\Longleftrightarrow$

${\mathbf{0}\in V}$ .
${\boldsymbol{v},\,\boldsymbol{w}\in V}$ ならば ${\boldsymbol{v}+\boldsymbol{w}\in V}$ .
${\boldsymbol{v}\in V}$ , ${c\in\mathbb{R}}$ に対して， ${c\boldsymbol{v}\in V}$ .

線形写像 ${f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}}$ に対して， ${\mathrm{Ker}\, f}$ は ${\mathbb{R}^{n}}$ の， ${\mathrm{Im}\, f}$ は ${\mathbb{R}^{m}}$ の部分空間.

7.2. 基底と座標

定義7.2. (i) ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\in\mathbb{R}^{n}}$ の間の一次関係 (linear relation) ${c_{1}\boldsymbol{v}_{1}+\dots+c_{r}\boldsymbol{v}_{r}=\boldsymbol{0}}$ , ( ${c_{i}\in\mathbb{R}}$ )．自明な一次関係 ${0\boldsymbol{v}_{1}+\dots+0\boldsymbol{v}_{r}=\boldsymbol{0}}$ ．
(ii) ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\in\mathbb{R}^{n}}$ が非自明な線形関係を持たないとき， ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}}$ は一次独立 (linearly independent)であるという．逆に非自明な線形関係があるときには一次従属 (linearly dependent)であるという．
(iii) ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\in\mathbb{R}^{n}}$ が部分空間 ${W\subset\mathbb{R}^{n}}$ の基底 (basis)であるとは，次の2条件が成り立つこと．

${W=\mathrm{span}\{\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\}}$ ;
${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}}$ は一次独立である．

一次独立かどうかは次の補題で判定できる．

補題7.1. ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\in\mathbb{R}^{n}}$ に対して， ${A=\begin{pmatrix} \boldsymbol{v}_{1}\dots\boldsymbol{v}_{r} \end{pmatrix}}$ とおくとき，次の3条件は互いに同値:

${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}}$ は一次独立．
${\mathrm{Ker}\,A=\{\mathbf{0}\}}$ ．
${\mathrm{rank}(A)=r}$ ．

一方，基底の定義は次の言い換えを持つ．

命題7.1. 部分空間 ${V\subset\mathbb{R}^{n}}$ の部分集合 ${\{\boldsymbol{v}_{1}, \dots,\boldsymbol{v}_{r}\}}$ についての次の2条件は互いに同値である．

${\{\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\}}$ は ${V}$ の基底である．
任意の ${\boldsymbol{v}\in V}$ は ${\boldsymbol{v} =c_{1}\boldsymbol{v}_{1}+\dots+c_{r}\boldsymbol{v}_{r}}$ とただ一通りに書ける．

これから，基底に付随する座標が導入される．

定義7.3. ${V\subset\mathbb{R}^{n}}$ を部分空間として，その基底 ${\mathfrak{B}=\{\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\}}$ を取る．各 ${\boldsymbol{v}\in V}$ を

$\displaystyle \boldsymbol{v} =x_{1}\boldsymbol{v}_{1} +\dots+x_{r}\boldsymbol{v}_{r},\quad x_{i}\in\mathbb{R}$

と書いたとき，

$\displaystyle [\boldsymbol{v}]_{\mathfrak{B}} =\begin{pmatrix} x_{1}\\ \vdots\\ x_{r} \end{pmatrix}\in\mathbb{R}^{r}$

を ${\boldsymbol{v}\in V}$ の ${\mathfrak{B}}$ 座標ベクトル ( ${\mathfrak{B}}$ -coordinate vector)という．

6月20日次元

8.1. 部分空間の次元

補題8.1. ${V\subset\mathbb{R}^{n}}$ を部分空間とする．

${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{p}\subset V}$ が一次独立であり，
${V=\mathrm{span}\{\boldsymbol{w}_{1}, \dots, \boldsymbol{w}_{q}\}}$ であれば，

${p\leqq q}$ が成り立つ．

系8.1. 部分空間 ${V\subset \mathbb{R}^{n}}$ の基底の元の個数は，基底のとり方によらず一定である．

定義8.1. 部分空間 ${V\subset\mathbb{R}^{n}}$ の基底の要素の数を ${V}$ の次元 (dimension)と呼んで ${\dim V}$ と書く．

系8.2. 部分空間 ${V\subset \mathbb{R}^{n}}$ の次元を ${m}$ とする．
(i) ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{m}\in V}$ が一次独立なら， ${\{\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{m}\}}$ は ${V}$ の基底である．
(ii) ${V=\mathrm{span}\{\boldsymbol{v}_{1}, \dots, \boldsymbol{v}_{m}\}}$ なら， ${\{\boldsymbol{v}_{1},\dots, \boldsymbol{v}_{m}\}}$ は ${V}$ の基底である．

8.2. 像と核の基底

${m\times n}$ 行列 ${A}$ の核の基底は，階段行列による ${A\boldsymbol{x}=\boldsymbol{0}}$ の解法によって求められる．

定理8.1. 線形写像 ${f:\mathbb{R}^{n}\ni\boldsymbol{v}\mapsto A\boldsymbol{v}\in\mathbb{R}^{m}}$ の核の次元を ${\mathrm{null}(f)=\mathrm{null}(A)}$ と書くとき

$\displaystyle \mathrm{rank}(A)+\mathrm{null}(A)=n.$

命題8.1. ${m\times n}$ 行列 ${A}$ の ${j}$ 列ベクトルが軸列 (pivot column)であるとは， ${\mathrm{rref}(A)}$ の ${j}$ 列ベクトルがある行の最初の ${1}$ を含むこととする． ${A}$ の軸列の集合は ${\mathrm{Im}\,A}$ の基底である．

系8.3. ${\mathrm{rank}(A)=\dim(\mathrm{Im}\,A)}$ .

6月27日ベクトル空間

9.1. ベクトル空間

定義9.1. ベクトル空間 (vector space)とは，集合 ${V}$ とその要素 ${\boldsymbol{0}\in V}$ ，および写像

$\displaystyle V\times V\ni(\boldsymbol{v},\boldsymbol{w})\longmapsto\boldsymbol{v}+\boldsymbol{w}\in V,\quad\mathbb{R}\times V\ni(c,\boldsymbol{v})\longmapsto c\boldsymbol{v}\in V$

からなるデータで次の条件を満たすもの．

${\boldsymbol{u}+(\boldsymbol{v}+\boldsymbol{w})=(\boldsymbol{u}+\boldsymbol{v})+\boldsymbol{w}}$ , ( ${\boldsymbol{u}}$ , ${\boldsymbol{v}}$ , ${\boldsymbol{w}\in V}$ );
${\boldsymbol{v}+\boldsymbol{w} =\boldsymbol{w}+\boldsymbol{v}}$ , ( ${\boldsymbol{v}}$ , ${\boldsymbol{w}\in V}$ );
${\boldsymbol{v}+\boldsymbol{0}=\boldsymbol{v}}$ , ( ${\boldsymbol{v}\in V}$ );
${c(\boldsymbol{v}+\boldsymbol{w}) =c\boldsymbol{v} +c\boldsymbol{w}}$ , ( ${c\in\mathbb{R}}$ , ${\boldsymbol{v}}$ , ${\boldsymbol{w}\in V}$ );
${(c+d)\boldsymbol{v}=c\boldsymbol{v}+d\boldsymbol{v}}$ , ( ${c}$ , ${d\in\mathbb{R}}$ , ${\boldsymbol{v}\in V}$ );
${(cd)\boldsymbol{v}=c(d\boldsymbol{v})}$ , ( ${c}$ , ${d\in\mathbb{R}}$ , ${\boldsymbol{v}\in V}$ );
${1\boldsymbol{v}=\boldsymbol{v}}$ , ( ${\boldsymbol{v}\in V}$ ).

${\boldsymbol{v}\in V}$ が ${\boldsymbol{v}_{1},\dots, \boldsymbol{v}_{r}\in V}$ の一次結合であるとは，

$\displaystyle \boldsymbol{v}=c_{1}\boldsymbol{v}_{1} +\dots+c_{r}\boldsymbol{v}_{r},\quad c_{i}\in\mathbb{R}$

と書けること． ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\in V}$ の一次結合の集合を ${\mathrm{span}\{\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\}}$ と書く．

定義9.2. 線形空間 ${V}$ の部分空間とは，部分集合 ${W\subset V}$ で次の条件を満たすもの．

${\mathbf{0}\in W}$ .
${\boldsymbol{v},\,\boldsymbol{w}\in W}$ ならば ${\boldsymbol{v}+\boldsymbol{w}\in W}$ .
${\boldsymbol{v}\in W}$ , ${c\in\mathbb{R}}$ に対して， ${c\boldsymbol{v}\in W}$ .

定義9.3. ${V}$ をベクトル空間とする．
(i) ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\in V}$ の間の一次関係とは， ${c_{1}\boldsymbol{v}_{1}+\dots +c_{r}\boldsymbol{v}_{r}=0}$ , ( ${c_{i}\in\mathbb{R}}$ )の形の等式のこと． ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{r}\in V}$ が一次独立であるとは，それらが非自明な一次関係を持たないこと．
(ii) ${\mathfrak{B}=\{\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{n}\}\subset V}$ が ${V}$ の(有限) 基底であるとは， ${\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{n}}$ は一次独立で， ${V=\mathrm{span}\{\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{n}\}}$ が成り立つこと．このとき任意の ${\boldsymbol{v}\in V}$ は

$\displaystyle \boldsymbol{v}=c_{1}\boldsymbol{v}_{1}+\dots+c_{n}\boldsymbol{v}_{n},\quad c_{i}\in\mathbb{R}$

とただ一通りに書けるので， ${[\boldsymbol{v}]_{\mathfrak{B}}=\begin{pmatrix}c_{1}\\ \vdots\\ c_{n} \end{pmatrix}}$ とおいて，これを ${\boldsymbol{v}}$ の ${\mathfrak{B}}$ 座標ベクトルという．

定義9.4. 線形空間 ${V}$ が有限基底を持つとき，その基底の要素の個数は基底のとり方によらない．これを ${V}$ の次元と呼んで， ${\mathrm{dim}V}$ と書く． ${V}$ が有限基底を持たないときには， ${V}$ は無限次元である(infinite dimensional)という．

9.2. 線形写像

定義9.5. ベクトル空間 ${V}$ , ${W}$ の間の写像 ${f:V\rightarrow W}$ が線形写像であるとは，次の2条件を満たすこととする．

$\displaystyle f(\boldsymbol{u}+\boldsymbol{v})=f(\boldsymbol{u})+f(\boldsymbol{v}),\quad(\boldsymbol{u}, \boldsymbol{v}\in V);$

$\displaystyle f(c\boldsymbol{v})=cf(\boldsymbol{v}),\quad(c\in\mathbb{R}, \boldsymbol{v}\in V).$

このとき ${f}$ の像 ${\mathrm{Im}\, f\subset W}$ と核 ${\mathrm{Ker}\, f\subset V}$ を

$\displaystyle \mathrm{Im}\, f=\{f(\boldsymbol{v})\mid\boldsymbol{v}\in V\},\quad \mathrm{Ker}\, f=\{\boldsymbol{v}\in V\mid f(\boldsymbol{v})=\boldsymbol{0}\}$

と定める．特に ${\mathrm{Im}\, f}$ が有限次元のとき， ${\mathrm{rank}(f)=\dim(\mathrm{Im}\, f)}$ を ${f}$ の階数という．

定義9.6. 線形写像 ${f:V\rightarrow W}$ と ${V}$ の基底 ${\mathfrak{B}=(\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{n})}$ , および ${W}$ の基底 ${\mathfrak{C}=(\boldsymbol{w}_{1},\dots,\boldsymbol{w}_{m})}$ があるとき，

$\displaystyle f(\boldsymbol{v}_{j})=a_{1,j}\boldsymbol{w}_{1}+\dots+a_{m.j}\boldsymbol{w}_{m},\quad(1\leqq j\leqq n)$

となる ${a_{i,j}\in\mathbb{R}}$ がただ一通りに定まる:

$\displaystyle f(\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{n})=(\boldsymbol{w}_{1},\dots,\boldsymbol{w}_{m})\begin{pmatrix}a_{1,1} & \dots & a_{1,n}\\ \vdots & \ddots & \vdots\\ a_{m,1} & \dots & a_{m,n} \end{pmatrix}.$

この ${[f]_{\mathfrak{B},\mathfrak{C}}=\begin{pmatrix}a_{1,1} & \dots & a_{1,n}\\ \vdots & \ddots & \vdots\\ a_{m,1} & \dots & a_{m,n} \end{pmatrix}}$ を ${f}$ の ${(\mathfrak{B},\mathfrak{C})}$ 行列という．

7月4日内積と正規直交基底

10.1. 内積と正規直交基底

定義10.1. (a) ${\boldsymbol{v}=\begin{pmatrix} v_{1}\\ \vdots\\ v_{n} \end{pmatrix}}$ , ${\boldsymbol{w}=\begin{pmatrix} w_{1}\\ \vdots\\ w_{n} \end{pmatrix}\in\mathbb{R}^{n}}$ の内積 (inner product)を

$\displaystyle \boldsymbol{v}\cdot\boldsymbol{w} =v_{1}w_{1}+v_{2}w_{2}+\dots+v_{n}w_{n}\in\mathbb{R}$

と定める．
(b) ${\boldsymbol{v}}$ , ${\boldsymbol{w}\in \mathbb{R}^{n}}$ が直交している (orthogonal)とは， ${\boldsymbol{v}\cdot\boldsymbol{w}=0}$ であることとする．このことを ${\boldsymbol{v}\bot\boldsymbol{w}}$ と書き表す．
(c) ${\boldsymbol{v}\in\mathbb{R}^{n}}$ の長さ (length)を ${\|\boldsymbol{v}\|=\sqrt{\boldsymbol{v}\cdot \boldsymbol{v}}}$ と定める．長さが ${1}$ であるベクトルを単位ベクトル (unit vector)という．

定義10.2. ベクトル ${\boldsymbol{v}_{1},\dots, \boldsymbol{v}_{r}\in\mathbb{R}^{n}}$ が正規直交 (orthonormal)であるとは，2条件

${\|\boldsymbol{v}_{i}\|=1}$ , ( ${1\leq i\leq r}$ );
${\boldsymbol{v}_{i}\cdot\boldsymbol{v}_{j}=0}$ , ( ${1\leq i\not=j\leq r}$ )

を満たすこと．これらの条件はまとめて

$\displaystyle \boldsymbol{v}_{i}\cdot\boldsymbol{v}_{j} =\delta_{i,j}=\begin{cases} 1 & i=j\\ 0 & i\not=j \end{cases}$

とも書ける．この右辺の ${\delta_{i,j}}$ をKroneckerの ${\delta}$ 関数という．

命題10.1. (i)正規直交なベクトルの集合は一次独立である．
(ii)特に ${m}$ 次元部分空間 ${V\subset \mathbb{R}^{n}}$ の正規直交な部分集合 ${\{\boldsymbol{v}_{1}, \dots, \boldsymbol{v}_{m}\}\subset V}$ は ${V}$ の基底である．

10.2. 直交射影

命題10.2. 部分空間 ${V\subset \mathbb{R}^{n}}$ を取る．
(i) ${V^{\bot}=\{\boldsymbol{x}\in\mathbb{R}^{n}\mid\boldsymbol{x} \cdot \boldsymbol{v}=0,\,\boldsymbol{v}\in V\}}$ は ${\mathbb{R}^{n}}$ の部分空間である．これを ${V}$ の直交補空間 (orthogonal complement)という．
(ii) ${\left\{ \boldsymbol{u}_{1},\dots,\boldsymbol{u}_{m}\right\} }$ を ${V}$ の正規直交基底とする．任意の ${\boldsymbol{x}\in\mathbb{R}^{n}}$ に対して

$\displaystyle \mathrm{pr}_{V}(\boldsymbol{x}) =\sum_{j=1}^{r}\,(\boldsymbol{x}\cdot\boldsymbol{u}_{j})\boldsymbol{u}_{j}$

は ${\boldsymbol{x}-\mathrm{pr}_{V}(\boldsymbol{x})\in V^{\bot}}$ となるただ一つの ${V}$ の要素である．
(iii) ${\mathbb{R}^{n}\ni\boldsymbol{x}\mapsto\mathrm{pr}_{V}(\boldsymbol{x})\in V}$ は線形写像である．これを ${V}$ への直交射影 (orthogonal projection)という．

10.3. Cauchy-Schwarzの不等式

補題10.1. ${\boldsymbol{v}}$ と ${\boldsymbol{w}}$ が直交しているとき，

$\displaystyle \|\boldsymbol{v}+\boldsymbol{w}\|^{2} =(\boldsymbol{v}+\boldsymbol{w})\cdot(\boldsymbol{v}+\boldsymbol{w})=\|\boldsymbol{v}\|^{2}+2\boldsymbol{v}\cdot\boldsymbol{w}+\|\boldsymbol{w}\|^{2}$

$\displaystyle =\|\boldsymbol{v}\|^{2}+\|\boldsymbol{w}\|^{2}.$

系10.1. ${V\subset \mathbb{R}^{n}}$ を部分空間とするとき， ${\mathrm{pr}_{V}(\boldsymbol{x})\leqq\|\boldsymbol{x}\|}$ , ( ${\boldsymbol{x}\in\mathbb{R}^{n}}$ )．

命題10.3. ${\boldsymbol{x}}$ , ${\boldsymbol{y}\in \mathbb{R}^{n}}$ に対して， ${|\boldsymbol{x}\cdot\boldsymbol{y}| \leqq \|\boldsymbol{x}\|\|\boldsymbol{y}\|}$ ．

定義10.3. 余弦関数 ${\cos:[0,\pi] \rightarrow[-1,1]}$ は可逆である．その逆写像を ${\mathrm{Arccos}:[-1,1]\rightarrow[0,\pi]}$ と書く．これを用いて ${\boldsymbol{v}}$ , ${\boldsymbol{w}\not =\boldsymbol{0}}$ , ${\in\mathbb{R}^{n}}$ のなす角 ${\theta\in[0,\pi]}$ を

$\displaystyle \theta=\mathrm{Arccos} \frac{\boldsymbol{v}\cdot\boldsymbol{w}}{\|\boldsymbol{v}\|\|\boldsymbol{w}\|},$

と定める．

7月11日 Gram-Schmidt の直交化と $QR$ 分解

12.1. Gram-Schmidtの直交化

定理12.1. 部分空間 ${V\subset\mathbb{R}^{n}}$ の基底 ${\{\boldsymbol{v}_{1}, \dots,\boldsymbol{v}_{m}\}}$ に対して， ${V_{j}=\mathrm{span}\{\boldsymbol{v}_{1},\dots,\boldsymbol{v}_{j}\}}$ , ( ${1\leqq j\leqq m}$ )とおけば，漸化式

$\displaystyle \boldsymbol{u}_{1} =\frac{\boldsymbol{v}_{1}}{\|\boldsymbol{v}_{1}\|}, \quad \boldsymbol{u}_{j}=\frac{\boldsymbol{v}_{j}-\mathrm{pr}_{V_{j-1}}(\boldsymbol{v}_{j})}{\|\boldsymbol{v}_{j}-\mathrm{pr}_{V_{j-1}}(\boldsymbol{v}_{j})\|},\quad2\leqq j\leqq m$

により定まる ${\{\boldsymbol{u}_{1},\dots,\boldsymbol{u}_{m}\}}$ は ${V}$ の正規直交基底である．

系12.1. ${n\times m}$ 行列 ${A=\left(\boldsymbol{v}_{1}\boldsymbol{v}_{2}\dots \boldsymbol{v}_{m} \right)}$ が ${\mathrm{rank}(A)=m}$ を満たすならば，

${n\times m}$ 行列 ${Q=\left(\boldsymbol{u}_{1} \boldsymbol{u}_{2}\dots\boldsymbol{u}_{m} \right)}$ で ${\boldsymbol{u}_{1},\dots,\boldsymbol{u}_{m}}$ が正規直交であるものと，
${m}$ 次正方上三角 (upper triangular)行列 ${R=\begin{pmatrix}r_{1,1} & r_{1,2} & \dots & r_{1,m}\\ 0 & r_{2,2} & \ddots & \vdots\\ \vdots & \ddots & \ddots & r_{m-1,m}\\ 0 & \dots & 0 & r_{m,m} \end{pmatrix}}$

があって， ${A=QR}$ と書ける．

12.2. 直交行列と直交変換

定義12.1. 線形写像 ${f:\mathbb{R}^{n}\ni\boldsymbol{v}\mapsto A\boldsymbol{v}\in \mathbb{R}^{n}}$ が直交変換 (orthogonal transformation), あるいは ${A}$ が直交行列 (orthogonal matrix)であるとは，

$\displaystyle \|f(\boldsymbol{v})\|=\|\boldsymbol{v}\|, \quad \boldsymbol{v}\in\mathbb{R}^{n}$

が成り立つこととする．特に ${\mathrm{Ker} f=\{\boldsymbol{0}\}}$ だから，直交変換は可逆である．

補題12.1. 直交変換 ${f: \mathbb{R}^{n}\rightarrow\mathbb{R}^{n}}$ は内積を保つ: ${f(\boldsymbol{v})\cdot f(\boldsymbol{w})=\boldsymbol{v}\cdot \boldsymbol{w}}$ , ( ${\boldsymbol{v}}$ , ${\boldsymbol{w}\in\mathbb{R}^{n}}$ ).

命題12.1. (i) ${n}$ 次正方行列 ${A=\left(\boldsymbol{v}_{1}\boldsymbol{v}_{2}\dots\boldsymbol{v}_{n} \right)}$ が直交行列であるためには， ${\{\boldsymbol{v}_{1},\dots, \boldsymbol{v}_{n}\}}$ が ${\mathbb{R}^{n}}$ の正規直交基底であることが必要十分である．
(ii) ${n}$ 次の直交行列 ${A}$ , ${B}$ の積 ${AB}$ および逆行列 ${A^{-1}}$ は直交行列である．

定義12.2. (i) ${m\times n}$ 行列 ${A=\begin{pmatrix}a_{1,1} & \dots & a_{1,n}\\ \vdots & \ddots & \vdots\\ a_{m,1} & \dots & a_{m,n} \end{pmatrix}}$ の転置行列 (transpose)を

$\displaystyle {}^{t}A=\begin{pmatrix} a_{1,1} & \dots & a_{m,1} \\ \vdots & \ddots & \vdots \\ a_{1,n} & \dots & a_{m,n} \end{pmatrix}$

と定める．

系12.2. ${n}$ 次正方行列 ${A}$ が直交行列であるためには， ${^{t}AA=E_{n}}$ であることが必要十分である．

7月18日内積の応用

連絡事項：
- 期末テストについて
- 次回，授業アンケートを実施する．
内積の応用（スライド）

7月25日後半の復習

8月1日期末テスト

成績評価について

成績評価は中間，期末テストの結果を総合的に判断して行います．

中間テストについて

6月6日の授業の時間に中間テストを行いました．
範囲は，4月11日から5月23日までの授業内容と，4月18日から5月30日までの演習内容です．
ノートなどの持ち込みは禁止します．筆記具と計時機能のみの時計，学生証を忘れず持ってきてください．

期末テストについて

8月1日の授業の時間に期末テストを行いました．
範囲は6月13日から7月11日までの授業内容と，6月20日から7月18日までの演習内容です．
ノートなどの持ち込みは禁止します．筆記具と計時機能のみの時計，学生証を忘れず持ってきてください．

今野拓也のページ

研究、教育関連の情報など

線形代数学・同演習A (2018年度)

授業の日時，場所

教科書について

授業の進め方

履修のコツ

授業予定

4月11日掃き出しと線形方程式系

4月18日線型方程式系の解の構造

4月25日線形写像

5月2日金曜授業日

5月9日写像の合成と行列の積

5月16日可逆写像と逆行列

5月23日線形写像の像と核

5月30日前半の復習

6月6日中間テスト

6月13日 ${\mathbb{R}^{n}}$ の部分空間とその基底

6月20日次元

6月27日ベクトル空間

7月4日内積と正規直交基底

7月11日 Gram-Schmidt の直交化と $QR$ 分解

7月18日内積の応用

7月25日後半の復習

8月1日期末テスト

成績評価について

中間テストについて

期末テストについて

授業の日時，場所

教科書について

授業の進め方

履修のコツ

授業予定

4月11日 掃き出しと線形方程式系

4月18日 線型方程式系の解の構造

4月25日 線形写像

5月2日 金曜授業日

5月9日 写像の合成と行列の積

5月16日 可逆写像と逆行列

5月23日 線形写像の像と核

5月30日 前半の復習

6月6日 中間テスト

6月13日 の部分空間とその基底

6月20日 次元

6月27日 ベクトル空間

7月4日 内積と正規直交基底

7月11日 Gram-Schmidt の直交化と 分解

7月18日 内積の応用

7月25日 後半の復習

8月1日 期末テスト

成績評価について

中間テストについて

期末テストについて

4月11日掃き出しと線形方程式系

4月18日線型方程式系の解の構造

4月25日線形写像

5月2日金曜授業日

5月9日写像の合成と行列の積

5月16日可逆写像と逆行列

5月23日線形写像の像と核

5月30日前半の復習

6月6日中間テスト

6月13日 ${\mathbb{R}^{n}}$ の部分空間とその基底

6月20日次元

6月27日ベクトル空間

7月4日内積と正規直交基底

7月11日 Gram-Schmidt の直交化と $QR$ 分解

7月18日内積の応用

7月25日後半の復習

8月1日期末テスト