代数学III (2019)

2019年9月19日12:39作成
2020年2月12日19:40更新

授業の日時，場所

火曜日2時限目
講義棟302号室

教科書

この授業は原則として次の教科書に沿って進めます。

代数学3 体とガロア理論
桂利行著
東京大学出版会

授業の進め方

授業は講義によります．講義だけでも履修可能ですが，ガロア理論を通じて触れる対称性や等質空間などの現代数学の考え方に慣れ親しむためには，授業中に出題する宿題を各自で解いてみることが非常に大切です．

授業内容

これはあくまでも予定であり，諸事情により変更になることがあります．

10月8日導入と復習

1.1. 導入—歴史の概要

1.2. 環の復習

(単位的)環とその部分環．
環 ${R}$ の単元群 ${R^{\times}}$
可換環と整域
可換環 ${R}$ のイデアル ${\mathfrak{a}}$ と商環 ${R/\mathfrak{a}}$
(環)準同型 ${f:R\rightarrow R'}$ と準同型定理
$\displaystyle R/\mathrm{Ker}f\overset{\sim}{\longrightarrow}\mathrm{Im} f$

1.3. 体の復習

体 (field)とは，環 ${(F,+,\cdot)}$ で ${(F\smallsetminus\{0\},\cdot)}$ がアーベル群であるもの．
(i) 体は特に整域である．
(ii)群は少なくとも単位元を含むから，体 ${F}$ に対して ${F\smallsetminus\{0\}\supset\left\{ 1\right\} }$ ．

補題零環でない可換環 ${R}$ が体 $\Longleftrightarrow$ ${R}$ のイデアルは ${\{0\}}$ と ${R}$ 自身しかない．特に，体の準同型 ${f:F\rightarrow F'}$ は常に単射．

例1 ${\mathbb{Q}}$ , ${\mathbb{R}}$ , ${\mathbb{C}}$ は体．また素数 ${p}$ に対して商環 ${\mathbb{F}_{p}:=\mathbb{Z}/p\mathbb{Z}}$ も体．

1.4. 素体と標数

${F}$ を体として，写像 ${\varphi:\mathbb{Z}\ni n\longmapsto n1_F\in F}$ を考える．

${\mathrm{Ker}\varphi=\{0\}}$ のとき， ${\varphi}$ は準同型
$\displaystyle \varphi:\mathbb{Q}\ni\frac{a}{b}\longmapsto(a\cdot1_{F})\cdot(b\cdot1_{F})^{-1}\in F$

に延びる．このとき ${F}$ は標数 (characteristic) ${0}$ で， ${\mathbb{Q}\overset{\varphi}{\hookrightarrow}F}$ はその素体 (prime field)．
${\mathrm{Ker}\varphi=p\mathbb{Z}}$ , ( ${p\in\mathbb{N}}$ )のとき， ${p}$ は素数で， ${\varphi}$ は
$\displaystyle \bar{\varphi}:\mathbb{Z}/p\mathbb{Z}\longrightarrow F$

に落ちる．このとき ${F}$ の標数は ${p}$ で， ${\mathbb{F}_{p}\overset{\bar{\varphi}}{\hookrightarrow}F}$ はその素体．

例 ${\mathbb{F}_{p}}$ のFrobenius自己同型．

10月15日体拡大

2.1. 多項式環の復習

体 ${F}$ を係数とする一変数多項式環
$\displaystyle F[x]=\{a_{m}x^{m}+a_{m-1}x^{m-1}+\dots+a_{0}\,|\,m\in\mathbb{N},\,a_{i}\in F\}$
${f(x)=a_{m}x^{m}+a_{m-1}x^{m-1}+\dots+a_{0}\in F[x]}$ , ${a_{m}\not=0}$ の次数 ${\deg f:=m}$ .
${f(x)}$ がモニック ${\quad \Longleftrightarrow \quad a_{m}=1}$ ．
環 ${R}$ が ${F}$ を含むとき， ${a\in R}$ に対する代入準同型
$\displaystyle F[x]\ni f(x)\longmapsto f(a)\in R$

除法の原理 ${\forall f(x),\,\forall g(x)\in F[x]}$ , ${g(x)\not=0}$ ， ${\exists !q(x), \exists !r(x)\in F[x]}$

${f(x)=q(x)g(x)+r(x)}$ ;
${\deg r<\deg g}$ .

${q(x)}$ ；商 (quotient), ${r(x)}$ ；余り (剰余，residue)．

帰結

(因数定理) ${f(x)\in F[x]}$ が ${\alpha\in F}$ を根に持つ: ${f(\alpha)=0}$ ${\quad \Longleftrightarrow \quad f(x)}$ が ${x-\alpha}$ で割り切れる．
従って ${f(x)\in F[x]}$ の ${F}$ 内の根は高々 ${\deg f}$ 個．
${F[x]}$ はEuclid整域なので単項イデアル整域 (PID)．
特に ${F[x]}$ は一意分解整域 (UFD)．

2.2. 多項式の既約性

Gaussの補題. ${f(x)\in\mathbb{Z}[x]}$ が既約であるためには，それが ${\mathbb{Q}[x]}$ の元として既約なことが必要十分．

補題2.2. 既約分数 ${r=\dfrac{c}{d}\in\mathbb{Q}}$ が ${a_{m}x^{m}+a_{m-1}x^{m-1}+\dots+a_{0}\in\mathbb{Z}[x]}$ の根ならば， ${c|a_{0}}$ かつ ${d|a_{m}}$ ．

これだけでも特別な3次式の既約性が判定できる．

命題2.1 (Eisensteinの判定律). ${f(x)=a_{m}x^{m}+a_{m-1}x^{m-1}+\dots+a_{0}\in\mathbb{Z}[x]}$ が，ある素数 ${p}$ に対して

$\displaystyle p\nmid a_{m},\quad p\mid a_{i},\ (0\leq i\leq m-1),\quad p^{2}\nmid a_{0}$

を満たせば ${f(x)\in\mathbb{Q}[x]}$ は既約．

2.3. 体拡大

定義 2.1. ${F}$ が体 ${E}$ の部分体のとき， ${E}$ を ${F}$ の拡大体 (extension field)と呼ぶ．記号： ${E/F}$ .
${[E:F]:=\dim_{F}E}$ ； ${E/F}$ の(拡大) 次数 (degree)．

命題 2.2. ${L\supset E\supset F}$ ；体拡大の列．
(i) ${[L:F]<\infty\quad \Longleftrightarrow }$ ${\quad [L:E]<\infty}$ かつ ${[E:F]<\infty}$ .
(ii) そのとき ${[L:F]=[L:E][E:F]}$ .

2.4. 体の生成

定義 2.2. ${E/F}$ ；体拡大， ${S\subset E}$ ；部分集合．

$\displaystyle F[S]:=\bigcap_{\substack{R\subset E; F\text{-subalg.} \\ R\supset F,R\supset S } }\,R$

を ${S}$ で生成される (部分) ${F}$ 代数，

$\displaystyle F(S):=\bigcap_{\substack{K\subset E\text{ ; subfield}\\ K\supset F,K\supset S } }\,K$

を ${F}$ 上で ${S}$ により生成される部分体という．
${S}$ が部分体 ${F'\subset E}$ のとき ${F(F')}$ を ${F}$ と ${F'}$ の合成体 (composite)と呼び， ${F.F'}$ と書く．
${S}$ が有限集合 ${\left\{ r_{1},\dots,r_{m}\right\} }$ のとき

$\displaystyle F[r_{1},\dots,r_{m}]:=F[S],\quad F(r_{1},\dots,r_{m}):=F(S)$

補題 2.4. 体 ${F}$ を含む整域 ${R}$ が ${F}$ 上有限次元なら， ${R}$ は体．

定義 2.3. ${E/F}$ ；体拡大． ${\alpha\in E}$ に対して ${F(\alpha)/F}$ の形の拡大を単純拡大(simple extension)という．

10月22日即位礼正殿の儀

10月24日（木曜日！）代数拡大と超越拡大

3.1. 代数元と超越元

${E/F}$ ；体拡大， ${\alpha\in E}$ ．代入準同型

$\displaystyle \varphi_{\alpha}:F[x]\ni f(x)\longmapsto f(\alpha)\in E$

${\mathrm{Ker} \varphi_{\alpha}=\{0\}}$ のとき， ${\varphi_{\alpha}}$ は分数体の同型
$\displaystyle \varphi_{\alpha} : F(x)\overset{\sim}{\longrightarrow} F(\alpha)$

に延びて， ${\alpha}$ は ${F}$ 上で超越的 (transcendental)．
のとき．；モニック多項式 s.t. ．体の埋め込み．
1. ${\bar{\varphi}_{\alpha}:F[x]/(f_{\alpha}(x))\overset{\sim}{\rightarrow} F(\alpha)}$ は同型で， ${F(\alpha)= F[\alpha]}$ ． ${f_{\alpha}(x)\in F[x]}$ は既約．
2. ${[F(\alpha):F]=\deg f_{\alpha}}$ ．
このとき ${\alpha}$ は ${F}$ 上代数的 (algebraic)． ${f_{\alpha}(X)}$ ； ${\alpha}$ の ${F}$ 上の最小多項式 (minimum polynomial)．

定義 3.1. ${E/F}$ ；体拡大が代数的とは，任意の ${\alpha\in E}$ が ${F}$ 上代数的なこと．そうでない時， ${E/F}$ は超越的であるという．

命題 3.1. 体拡大 ${E/F}$ が有限次． $\Longleftrightarrow$ ${E/F}$ は代数拡大で， ${E}$ は有限生成 ${F}$ 代数．

系 3.1.　(a) ${E/F}$ が代数拡大なら， ${E\supset R\supset F}$ なる部分環 ${R}$ は体．
(b) ${L/E}$ , ${E/F}$ が代数的なら ${L/F}$ も代数拡大．

3.2. 代数閉体 ．

多項式 ${f(x)\in F[x]}$ が分解する(split)とは，それが一次式の積に分解すること．

命題 3.2. 体 ${\Omega}$ について次の4条件は互いに同値．

任意の ${f(x)\in\Omega[x]\smallsetminus\Omega}$ は分解する．
任意の ${f(x)\in\Omega[x]\smallsetminus\Omega}$ は ${\Omega}$ 内に少なくとも一つの根をもつ．
${\Omega[x]}$ の既約元は一次式である．
${\Omega}$ の有限次拡大は ${\Omega}$ 自身だけである．

定義 3.2. 体 ${\Omega}$ は命題3.2の条件をみたすとき，代数閉体 (algebraically closed field)と呼ばれる．体 ${F}$ の代数閉包 (algebraic closure)とは，代数拡大 ${\Omega/F}$ で代数閉体であるもの．

補題 3.1.　代数拡大 ${\Omega/F}$ で，任意の ${f(x)\in F[x]}$ が ${\Omega[x]}$ で分解するものは ${F}$ の代数閉包．

10月29日分解体

4.1. 分解体

定義 4.1. (i) 拡大 ${E/F}$ が ${f(x)}$ を分解 ${\quad \Longleftrightarrow\quad f(x)}$ が ${E[x]}$ で分解．

(ii)さらに ${E}$ が ${f(x)}$ の根で ${F}$ 上生成されるとき， ${E}$ を ${f(x)\in F[x]}$ の(最小) 分解体 (splitting field)という．

命題 4.1. (i)任意の ${f(x)\in F[x]}$ の分解体 ${E_{f}/F}$ が存在．

(ii) ${[E_{f}:F]\leq(\deg f(x))!}$ ．

4.2. 準同型の延長

命題 4.2. ${F(\alpha)/F}$ ；単純拡大， ${\Omega/F}$ ；拡大．

(i) ${\alpha}$ が ${F}$ 上超越的なら，次は全単射．

$\displaystyle \mathrm{Hom}_{F\text{-alg}}(F(\alpha),\Omega)\ni\varphi\longmapsto\varphi(\alpha) \in\{ \beta\in \Omega \mid \text{transcendental over }F\}.$

(ii) ${\alpha}$ が ${F}$ 上代数的なとき，その最小多項式を ${f_{\alpha}(x)\in F[x]}$ として，次は全単射．

$\displaystyle \mathrm{Hom}_{F\text{-alg}}(F(\alpha),\Omega) \ni\varphi \longmapsto\varphi(\alpha) \in\{ \beta\in \Omega\mid f_{\alpha}(\beta)=0\}.$

${\sigma : F\rightarrow F'}$ ；体の同型， ${f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\dots+a_{0}\in F[x]}$ に対して
$\displaystyle \sigma(f)(x):= \sigma(a_{n})x^{n}+\sigma(a_{n-1})x^{n-1}+\dots+\sigma(a_{0})\in F'[x].$

命題 4.3. ${E/F}$ ；多項式 ${f(x)\in F[x]}$ の根(の一部) ${\alpha_{1},\dots,\alpha_{r}\in E}$ で生成される拡大． ${\sigma:F\rightarrow F'}$ ；同型． ${\Omega/F'}$ ； ${\sigma(f)(x)\in F'[x]}$ を分解する拡大．

(i) ${0<|\left\{ \varphi\in\mathrm{Hom}(E,\Omega)\mid\varphi|_{F} =\sigma\right\} |\leq[E:F]}$ ．さらに ${f(x)}$ が ${\deg f}$ 個の異なる根を持てば後半は等式．

(ii)さらに ${E}$ , ${\Omega}$ がそれぞれ ${f(x)\in F[x]}$ , ${\sigma(f)(x)\in F'[x]}$ の最小分解体なら， ${\varphi|_{F}=\sigma}$ となる ${\varphi\in \mathrm{Hom}(E,\Omega)}$ はすべて同型．特に ${f(x)\in F[x]}$ の最小分解体は同型を除いて一意．

系 4.1. ${E/F}$ ；有限次拡大．

(i)任意の体拡大 ${L/F}$ に対して， ${|\mathrm{Hom}_{F\text{-alg}}(E,L)|\leq [E:F]}$ .

(ii)その有限次拡大 ${K/L}$ で ${\mathrm{Hom}_{F\text{-alg}}(E,K)\not=\varnothing}$ となるものがある．

11月5日分離拡大

5.1. 重根

${f(x)\in F[x]}$ , ${E_{f}/F}$ ；その分解体．
$\displaystyle f(x)=a\prod_{i=1}^{r}\,(x-\alpha_{i})^{m_{i}},\quad\alpha_{i}\not=\alpha_{j},\,\in E_{f}$

このとき ${\alpha_{i}}$ が ${f}$ の単根 (simple root)　 $\quad \Longleftrightarrow \quad {m_{i}=1}$ .
そうでないとき ${\alpha_{i}}$ は重根 (multiple root)．

命題 5.1. 既約多項式 ${f(x)\in F[x]}$ について次の4条件は互いに同値．

${f(x)}$ は重根を持つ．
${f(x)}$ と ${f'(x)}$ は非自明な共通因子を持つ.
${F}$ は正標数 ${p}$ を持ち， ${f(x)\in F[x^{p}]}$ .
${f(x)}$ の根はすべて重根．

定義 5.1. (i) ${f(x)\in F[x]}$ が分離的 (separable) $\Longleftrightarrow$ 任意の既約因子が重根を持たない．
(ii)体 ${F}$ が完全 (perfect)とは， ${F[x]}$ の任意の元が分離的であること．

5.2. 体の自己同型群

環 ${A}$ の自己同型群 ${\mathrm{Aut}(A)}$ ． ${A}$ が ${F}$ 代数のとき， ${A}$ の ${F}$ 代数自己同型群:
$\displaystyle \mathrm{Aut}_{F\text{-alg}}(A):=\left\{ \varphi\in\mathrm{Aut}(A)\mid\varphi|_{F}=\mathrm{id}_{F}\right\}$

命題 5.2. 分離的な ${f(x)\in F[x]}$ の最小分解体を ${E_{f}/F}$ とすれば， ${|\mathrm{Aut}_{F\text{-alg}}(E_{f})|=[E_{f}:F]}$ ．

5.3. 固定体

定義 5.2. ${E}$ ；体， ${G\subset\mathrm{Aut}(E)}$ ；部分群

$\displaystyle E^{G}:=\{x\in E\,|\,\sigma(x)=x,\,\sigma\in G\}$

を ${G}$ の固定体 (fixed field)と呼ぶ．

$\displaystyle |G|\leq|\mathrm{Aut}_{E^{G}\text{-alg}}(E)|\leq[E:E^{G}] \ \ \ \ \ (1)$

命題 5.3 (E. Artin).　有限部分群 ${G\subset\mathrm{Aut}(E)}$ に対して ${[E:E^{G}]=|G|}$ ．

系 5.1. 有限部分群 ${G\subset\mathrm{Aut}(E)}$ に対して ${\mathrm{Aut}_{E^{G}\text{-alg}}(E)=G}$ ．

11月12日ガロア理論の基本定理

6.1. ガロア拡大

定義 6.1. (i)代数拡大 ${E/F}$ が分離的 (separable)とは，任意の ${\alpha\in E}$ の ${F}$ 上の最小多項式が分離多項式であること．
(ii)代数拡大 ${E/F}$ が正規 (normal)とは，任意の ${\alpha\in E}$ の ${F}$ 上の最小多項式が ${E}$ で分解すること．

定理 6.1. 体拡大 ${E/F}$ について次の4条件は同値である．

${E}$ はある分離多項式 ${f(x)\in F[x]}$ の最小分解体．
${[E:F]<\infty}$ で， ${\mathrm{Aut}_{F\text{-alg}}(E)}$ の固定体は ${F}$ ．
ある有限部分群 ${G\subset\mathrm{Aut}(E)}$ があって ${F=E^{G}}$ .
${E/F}$ は有限次正規分離拡大．

定義 6.2. (i)有限次代数拡大 ${E/F}$ がガロア (Galois) 拡大であるとは，それが定理2の互いに同値な4条件を満たすこと．
そのとき ${\mathrm{Aut}_{F\text{-alg}}(E)}$ を ${E/F}$ のガロア群 (Galois group)と呼んで ${\mathrm{Gal}(E/F)}$ と書く．また ${\alpha\in E}$ の ${\mathrm{Gal}(E/F)}$ 軌道

$\displaystyle \mathrm{Gal}(E/F)\alpha=\left\{ \sigma(\alpha)\mid\sigma\in\mathrm{Gal}(E/F)\right\} \subset E$

の元を ${\alpha}$ の共役元 (conjugate)という．
(ii)有限次ガロア拡大 ${E/F}$ がアーベル拡大 (abelian extension)とは， ${\mathrm{Gal}(E/F)}$ がアーベル群であること．さらに ${\mathrm{Gal}(E/F)}$ が巡回群のとき， ${E/F}$ は巡回拡大 (cyclic extension)であるという．

系 6.1. (i)任意の有限次分離拡大 ${E/F}$ を含む有限次ガロア拡大が存在．

(ii)体拡大の列 ${K\supset E\supset F}$ において ${K/F}$ がガロア拡大なら， ${K/E}$ もガロア拡大．

6.2. ガロア理論の基本定理

${K\supset E\supset F}$ ；拡大列． ${E}$ を拡大 ${K/F}$ の中間体 (intermediate field)という．

定理 6.2 (ガロア理論の基本定理).　(1) ${K/F}$ ；ガロア拡大．

$\displaystyle \left\{\begin{array}{l} \text{Subgroups of} \\ \mathrm{Gal}(K/F)\end{array}\right\} \ni \begin{array}{ccc} \Theta & \mapsto & K^{\Theta}\\ \mathrm{Gal}(K/E) & \mapsfrom & E \end{array} \in\left\{\begin{array}{l} \text{intermediate} \\ \text{fields of }K/F \end{array}\right\}$

は全単射で互いの逆写像．
(2)さらにこの全単射は次の性質を持つ．

包含関係を逆転: ${\Theta\subset\Xi\subset\mathrm{Gal}(K/F)}$ ${\Leftrightarrow}$ ${K^{\Theta}\supset K^{\Xi}\supset F}$ .
次数は指数： ${\Theta\subset\Xi\subset\mathrm{Gal}(K/F)}$ のとき， ${[K^{\Theta}:K^{\Xi}]=[\Xi:\Theta]}$ ．
${\mathrm{Gal}(K/F)}$ 同変： ${\forall \sigma\in \mathrm{Gal}(E/F)}$ ， ${\forall\Theta\subset\mathrm{Gal}(E/F)}$ ；部分群に対して， ${\sigma(K^{\Theta})=K^{\sigma\Theta\sigma^{-1}}}$ ．
中間体 ${K\supset E\supset F}$ が ${F}$ のガロア拡大であるためには， ${\mathrm{Gal}(K/E)}$ が ${\mathrm{Gal}(K/F)}$ の正規部分群であることが必要十分，そのとき
$\displaystyle \mathrm{Gal}(K/F)/\mathrm{Gal}(K/E)\ni\sigma\mathrm{Gal}(K/E)\longmapsto\sigma|_{E}\in\mathrm{Gal}(E/F)$

は同型．

11月19日ガロア群の計算

7.1. 初等的な例

例7.1. ${\zeta=\zeta_{7}:=e^{2\pi i/7}\in\mathbb{C}}$ の ${\mathbb{Q}}$ として， ${\mathbb{Q}(\zeta)/\mathbb{Q}}$ のガロア群と中間体．

命題 7.1 (推進定理). 拡大 ${\Omega/F}$ の有限次中間体 ${E/F}$ , ${K/F}$ を取る．

(i) ${E/F}$ がガロア拡大なら， ${E.K/K}$ , ${E/E\cap K}$ もガロア拡大．

(ii)そのとき ${\mathrm{Gal}(E.K/K)\ni\sigma\mapsto\sigma|_{E}\in\mathrm{Gal}(E/E\cap K)}$ は同型．

例7.2. ${x^5 -2\in \mathbb{Q}[x]}$ の分解体のガロア群．

7.2. 多項式のガロア群

${n}$ 次の対称群 ${S_{n}}$ ． ${n}$ 変数の差積
$\displaystyle \Delta(x_{1},\dots,x_{n}):=\prod_{1\leq i<j\leq n}\,(x_{i}-x_{j})\in F[x_{1},\dots,x_{n}].$

対称群の符号指標 ${\mathrm{sgn} :S_{n}\rightarrow\{\pm1\}}$ と ${n}$ 次交代群 ${A_{n}}$ ．
${f(x)\in F[x]}$ ；モニックで重根を持たない多項式の分解体 ${E/F}$ のガロア群 ${G_{f}:=\mathrm{Gal}(E/F)}$ .
$\displaystyle f(x)=\prod_{i=1}^{n}\,(x-\alpha_{i}),\quad\alpha_{i}\in E$

と分解して，単射準同型 ${s:\mathrm{Gal}(E/F)\rightarrow S_{n}}$ :

$\displaystyle \sigma(\alpha_{i})=\alpha_{s(\sigma)^{-1}(i)},\quad1\leq i\leq n$

により， ${G_{f}}$ を ${s(G_{f})\subset S_{n}}$ と同一視．
${f(x)}$ の判別式:
$\displaystyle D_{f}:=\Delta_{f}^{2},\quad\Delta_{f}:=\Delta(\alpha_{1},\dots,\alpha_{n})\in E$

命題7.2. ${D_{f}\in F}$ で， ${E^{G_{f}\cap A_{n}}=F(\Delta_{f})}$ ．

補題7.1. ${G_{f}}$ が ${f(x)}$ の根の集合 ${\left\{ \alpha_{1},\dots,\alpha_{n}\right\} }$ に推移的に作用するためには， ${f(x)\in F[x]}$ が既約であることが必要十分．

11月26日ガロア群の計算2

8.1. 3次式と4次式

3次式のガロア群
${D_{f}=-4b^{3}-27c^{2}}$ が平方数か否かにより， ${A_3}$ か ${S_3}$ になる．

4次式のガロア群

の推移部分群は次の通り．
- ${S_{4}\triangleright A_{4}\triangleright V}$ . ただし ${V:=\left\{ 1,(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)\right\} \simeq (\mathbb{Z}/2\mathbb{Z})^{2}}$ はKleinの四元群． ${A_{4}}$ は ${\mathbb{R}^{3}}$ の中の正四面体の合同変換群(正四面体群)．
- 二面体群 ${D_{4}}$ : ${H_{\alpha}:=\left\langle (1,3,2,4),(1,2)\right\rangle }$ , ${H_{\beta}:=\left\langle (1,2,3,4),(1,3)\right\rangle }$ , ${H_{\gamma}:=\left\langle (1,2,4,3),(1,4)\right\rangle }$ .
  $\displaystyle H_{\alpha}\cap H_{\beta}\cap H_{\gamma}=V.$
- 4次巡回群 ${C_{\bullet}\subset H_{\bullet}}$ ．
；既約モニック分離4次式．, ()として，
$\displaystyle \alpha:=\alpha_{1}\alpha_{2}+\alpha_{3}\alpha_{4},\quad\beta:=\alpha_{1}\alpha_{3}+\alpha_{2}\alpha_{4},\quad\gamma:=\alpha_{1}\alpha_{4}+\alpha_{2}\alpha_{3}$
1. ${S_{4}}$ は ${\left\{ \alpha,\beta,\gamma\right\} }$ に推移的に作用．固定化群は ${(S_{4})_{\alpha}=H_{\alpha}}$ , ${(S_{4})_{\beta}=H_{\beta}}$ , ${(S_{4})_{\gamma}=H_{\gamma}}$ ．
${K:=E^{G_{f}\cap V}=F(\alpha,\beta,\gamma)}$ .
の分解三次式 (resolvent cubic)
$\displaystyle g(x):=(x-\alpha)(x-\beta)(x-\gamma)$

$\displaystyle =x^{3}-cx^{2}+(bd-4e)x-b^{2}e+4ce-d^{2}$
1. ${[G_{f}:G_{f}\cap V]=[K:F]\not=2}$ ならその値から， ${G_{f}}$ は決まる．
2. のとき．
  1. ${f(x)\in K[x]}$ が既約なら， ${G_{f}=H_{\bullet} \simeq D_{4}}$ .
  2. そうでなければ， ${G_{f}\simeq C_{\bullet}\simeq \mathbb{Z}/4\mathbb{Z}}$ .
8.2. 有限体

定理 8.1. ${p}$ ；素数．
(i) ${\forall n\in\mathbb{N}}$ に対して ${q=p^{n}}$ 個の元からなる体 ${\mathbb{F}_{q}}$ が同型を除いてただ1つ存在．それは ${x^{q}-x\in\mathbb{F}_{p}[x]}$ の最小分解体．
(ii) ${\mathbb{F}_{q}}$ は素体 ${\mathbb{F}_{p}}$ 上の ${n}$ 次巡回拡大で，そのガロア群はフロベニウス自己同型 ${\sigma=\mathrm{Frob}_{p}:\mathbb{F}_{q}\ni a\mapsto a^{p}\in\mathbb{F}_{q}}$ で生成される．

系 8.1. ${n\in\mathbb{N}}$ ， ${q=p^{n}}$ ．
(i) ${n}$ の任意の約数 ${d}$ に対して， ${\mathbb{F}_{q}/\mathbb{F}_{p}}$ の中間体 ${E}$ で ${p^{d}}$ 個の元からなるものがただ一つある．
(ii) ${\mathbb{F}_{q}/\mathbb{F}_{p}}$ の中間体は全てこうして得られる．

系 8.2. ${n\in\mathbb{N}}$ ．次数 ${d}$ が ${n}$ の約数である既約多項式 ${f(x)\in\mathbb{F}_{p}[x]}$ は ${x^{p^{n}}-x}$ の素因子．

系 8.3. 有限体 ${\mathbb{F}_{p}}$ の代数閉包が存在する．

12月3日ガロア理論の応用

9.1. 有理数体のガロア拡大の例

命題 9.1. ${F}$ ；体． ${f(x)\in F[x]}$ ；重根を持たないモニック多項式， ${E}$ ；その分解体， ${\left\{ \alpha_{1},\dots,\alpha_{n}\right\} \subset E}$ ； ${f(x)}$ の根

$\displaystyle \left\{ \alpha_{1},\dots,\alpha_{n}\right\} =\coprod_{i=1}^{r}\,O_{i}$

を ${G_{f}=\mathrm{Gal}(E/F)}$ による軌道分解とすると， ${f_{i}(x):=\prod_{\alpha\in O_{i}}\,(x-\alpha)}$ は ${F[x]}$ に属し

$\displaystyle f(x)=\prod_{i=1}^{r}\,f_{i}(x)$

は ${F[x]}$ での既約分解．

事実 9.1. ${p}$ ；素数， ${f(x)\in\mathbb{Z}[x]}$ ；モニック多項式 s.t. ${\bar{f}(x):=(f(x)\pmod{p})\in\mathbb{F}_{p}[x]}$ は重根を持たない．
${E/\mathbb{Q}}$ ； ${f(x)}$ の最小分解体， ${k/\mathbb{F}_{p}}$ ； ${\bar{f}(x)}$ の最小分解体．
(i) ${f(x)}$ の根 ${\alpha_{1},\dots,\alpha_{n}}$ は ${E}$ での ${\mathbb{Z}}$ の整閉包 ${R}$ に含まれる．
(ii) ${\exists \mathfrak{p}\subset R}$ ；素イデアル s.t. ${R/\mathfrak{p}\simeq k}$ ．
(iii) ${\bar{\alpha}_{i}:=(\alpha_{i}\pmod{\mathfrak{p}})}$ , ( ${1\leq i\leq n}$ )は ${\bar{f}(x)}$ の根で， ${\{ \alpha_{1},\dots,\alpha_{n}\} }$ と ${\{ \bar{\alpha}_{1}, \dots, \bar{\alpha}_{n}\} }$ の対称群を同一視すると， ${\mathrm{Gal}(k/\mathbb{F}_{p})\subset G_{f}}$ ．
- ${n}$ 次対称群 ${S_{n}}$ 内の共役類は ${n}$ の分割と一対一に対応する．
定理 9.1 (Dedekind). ${f(x)\in\mathbb{Z}[x]}$ ；モニック多項式， ${p}$ ；素数 s.t.
1. 法 ${p}$ 還元 ${\bar{f}(x):=(f(x)\pmod{p})\in\mathbb{F}_{p}[x]}$ は重根を持たない．
2. ${\mathbb{F}_{p}[x]}$ での既約分解 ${\bar{f}(x)=\prod_{i=1}^{r}\,\bar{f}_{i}(x)}$ がある．ここで ${d_{i}:=\deg\bar{f}_{i}(x)}$ とおく．
このとき， ${G_{f}}$ は ${(d_{1},\dots,d_{r})}$ 型の置換を含む．

例 9.1. ${S_{n}}$ をGalois群に持つ多項式の例．

9.2. 原始元
- 単純代数拡大 ${E/F}$ に対し， ${E=F(\alpha)}$ となる ${\alpha\in E}$ を ${E/F}$ の原始元 (primitive element)という．
定理 9.2. 有限次拡大 ${E=F(\alpha_{1},\dots,\alpha_{r})}$ で， ${\alpha_{2},\dots,\alpha_{r}}$ が ${F}$ 上で分離的なら， ${E/F}$ の原始元が存在．特に ${E/F}$ は単純拡大．

例 9.2. (i) Galois拡大の原始元の見つけ方．
(ii) 原始元がない有限次拡大の例．

12月10日ガロア理論の応用2

10.1. 円分拡大
- ${F}$ ；体． ${n\in \mathbb{N}}$ に対して， ${\zeta\in F^{\times}}$ が ${1}$ の原始 ${n}$ 乗根 (primitive ${n}$ -th root of unity)とは， ${\left\langle \zeta\right\rangle\simeq \mathbb{Z}/n\mathbb{Z}}$ であること．
- 定義から ${1}$ の原始 ${n}$ 乗根は高々 ${\varphi(n):=|(\mathbb{Z}/n\mathbb{Z})^{\times}|}$ 個．
命題 10.1. ${n\in\mathbb{N}}$ ， ${F}$ ；標数が ${n}$ を割りきらない体． ${E/F}$ ； ${x^{n}-1\in F[x]}$ の最小分解体．
(i) ${E}$ は ${1}$ の原始 ${n}$ 乗根 ${\zeta}$ を含み， ${E=F(\zeta)}$ ．
(ii) ${E/F}$ はガロア拡大で， ${\chi:\mathrm{Gal}(E/F)\rightarrow(\mathbb{Z}/n\mathbb{Z})^{\times}}$ を ${\sigma(\zeta)=\zeta^{\chi(\sigma)}}$ で定めれば，これは定義可能な単射準同型．
- 次円分多項式 (cyclotomic polynomial)を次の漸化式によって定める．
  1. ${\Phi_{1}:=x-1}$
  2. ${n>1}$ のとき，
    $\displaystyle \Phi_{n}(x):=\frac{x^{n}-1}{\prod_{d|n,\,d\not=n}\,\Phi_{d}(x)}.$
- ${x^{n}-1=\prod_{d|n}\,\Phi_{d}(x)}$ ，
  $\displaystyle \Phi_{n}(x)=\prod_{k\in(\mathbb{Z}/n\mathbb{Z})^{\times}}\,(x-\zeta_{n}^{k}),\quad\zeta_{n}=\exp\left(\frac{2\pi i}{n}\right)$
  
  特に ${\deg\Phi_{n}(x)=\varphi(n)}$ ．
命題 10.2. (Gaussの補題の別版) モニック多項式 ${f(x)\in\mathbb{Z}[x]}$ のモニックな因子は ${\mathbb{Z}[x]}$ に属する．

定理 10.1 (Dedekind). ${\Phi_{n}(x)}$ は ${\mathbb{Q}[x]}$ の既約元．特に

$\displaystyle \chi:\mathrm{Gal}(\mathbb{Q}(\zeta_{n})/\mathbb{Q})\longrightarrow(\mathbb{Z}/n\mathbb{Z})^{\times}$

は同型．

10.2. 指標の線型独立性

定理 10.2 (Dedekind). ${F}$ ；体， ${G}$ ；群のとき，任意の ${\{ \chi_{1},\dots,\chi_{n}\} \subset\mathrm{Hom}(G,F^{\times})}$ は ${F}$ 線型独立．

系 10.1.　体 ${E}$ , ${F}$ に対して，任意の ${\{ \varphi_{1},\dots,\varphi_{n}\} \subset\mathrm{Hom}(F,E)}$ は ${F}$ 線型独立．

10.3. 正規底

定理 10.3 (正規底定理). ${E/F}$ ；ガロア拡大． ${E}$ の ${F}$ 基底として ${\left\{ \sigma(\alpha)\mid\sigma\in\mathrm{Gal}(E/F)\right\} }$ , ( ${\alpha\in E}$ )の形のものが取れる (正規底 (normal basis))．

12月17日群コホモロジー

11.1. 鎖複体

定義 11.1. ${\Gamma}$ ；群．
(i) ${\Gamma}$ を基底とする加法群 ${\mathbb{Z}[\Gamma]=\{\sum_{\sigma\in\Gamma}\,m_{\sigma}\sigma\mid m_{\sigma}\in\mathbb{Z}\}}$ に

$\displaystyle \Bigl(\sum_{\sigma\in\Gamma}\,m_{\sigma}\sigma\Bigr)\Bigl(\sum_{\tau\in\Gamma}\,n_{\tau}\tau\Bigr)=\sum_{\tau\in\Gamma}\,\Bigl(\sum_{\sigma\in\Gamma}\,m_{\sigma}n_{\sigma^{-1}\tau}\Bigr)\tau$

と乗法を定めて得られる環を ${\Gamma}$ の群環 (group ring)という．
(ii)左 ${\mathbb{Z}[\Gamma]}$ 加群を ${\Gamma}$ 加群 ( ${\Gamma}$ -module)，それらの間の ${\mathbb{Z}[\Gamma]}$ 線型写像を ${\Gamma}$ 準同型 ( ${\Gamma}$ -homomorphism)と呼ぶ．
${\mathrm{Hom}_{\Gamma}(A,B)}$ ； ${\Gamma}$ 加群 ${A}$ から ${B}$ への ${\Gamma}$ 準同型からなるアーベル群．
- ${\Gamma}$ 鎖複体 ( ${\Gamma}$ -chain complex)　 ${C_{\bullet}=(\dots\overset{d_{n+1}}{\rightarrow}C_{n}\overset{d_{n}}{\rightarrow}C_{n-1}\overset{d_{n-1}}{\rightarrow}\dots)_{n\in\mathbb{Z}}}$ と，その ${n}$ 次ホモロジー群 ${\mathrm{H}_{n}(C_{\bullet}):=\mathrm{Ker} d_{n}/\mathrm{Im} d_{n+1}}$ ．
- ${\Gamma}$ 鎖写像 ( ${\Gamma}$ -chain map) ${f_{\bullet}:C_{\bullet}\rightarrow C'_{\bullet}}$ と付随するホモロジー群の準同型 ${\mathrm{H}_{n}(f_{\bullet}):\mathrm{H}_{n}(C_{\bullet})\rightarrow\mathrm{H}_{n}(C'_{\bullet})}$ ．後者は ${f_{\bullet}}$ のホモトピー同値類のみによる．
11.2. 射影分解

命題 11.1. ${\Gamma}$ 加群 ${P}$ について次の二条件は互いに同値．
1. ${\forall p : A\twoheadrightarrow B}$ ；全射 ${\Gamma}$ 準同型， ${\forall f : P\rightarrow B}$ ； ${\Gamma}$ 準同型， ${\exists\tilde{f}\in\mathrm{Hom}_{\Gamma}(P,A)}$ s.t.
2. ${P}$ はある自由 ${\Gamma}$ 加群の直和因子．
このとき， ${P}$ は射影的 (projective)．

命題 11.2. (i) ${\forall A}$ ； ${\Gamma}$ 加群は ${P_{\bullet}\overset{p}{\rightarrow}A}$ ；射影分解 (projective resolution), i.e. ${\dots P_{2}\overset{d_{2}}{\rightarrow}P_{1}\overset{d_{1}}{\rightarrow}P_{0}\overset{p}{\rightarrow}A\rightarrow0}$ ；完全系列 s.t. ${P_{n}}$ , ( ${n\geq0}$ )；射影的．
(ii) ${\forall Q_{\bullet}\overset{q}{\rightarrow}A}$ ；別の射影分解， ${\exists! f_{\bullet} : P_{\bullet}\rightarrow Q_{\bullet}}$ ； ${\Gamma}$ 鎖写像 (up to homotopy) s.t.

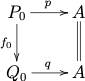
11.3. 群コホモロジー

定義11.2. ${A}$ , ${B}$ ； ${\Gamma}$ 加群， ${P_{\bullet}\overset{p}{\rightarrow}B}$ ；射影分解

$\displaystyle K^{n}:=\mathrm{Hom}_{\Gamma}(P_{n},A),\quad d^{n}:K^{n}\ni c\longmapsto c\circ d_{n+1}\in K^{n+1}$

${\Longrightarrow\quad K^{\bullet}=(0\rightarrow K^{0}\overset{d^{0}}{\rightarrow}K^{1}\overset{d^{1}}{\rightarrow}K^{2}\overset{d^{2}}{\rightarrow}\dots)}$ ；アーベル群の余鎖複体 (cochain complex)．
その ${n}$ 次コホモロジー群がExt群:

$\displaystyle \mathrm{Ext}_{\Gamma}^{n}(B,A):=\mathrm{H}^{n}(K^{\bullet}):=Z^{n}(K^{\bullet})/B^{n}(K^{\bullet}),$

$\displaystyle Z^{n}(K^{\bullet}):=\mathrm{Ker} d^{n},\quad B^{n}(K^{\bullet});=\mathrm{Im} d^{n-1}$

特に ${B=\mathbb{Z}}$ のとき，

$\displaystyle \mathrm{H}^{n}(\Gamma,A):=\mathrm{Ext}_{\Gamma}^{n}(\mathbb{Z},A)$

を ${A}$ 係数の ${n}$ 次 ${\Gamma}$ コホモロジー群 ( ${\Gamma}$ -cohomology group)という．

補題 11.1. ${\mathrm{Ext}_{\Gamma}^{n}(B,A)}$ , ( ${n\in\mathbb{Z}_{\geq0}}$ )は標準的: 一意な同型を除いて射影分解 ${P_{\bullet}\overset{p}{\rightarrow}B}$ の取り方によらない．

12月24日ガロアコホモロジー

12.1. 群コホモロジーの性質
- ${\Gamma}$ ；群，アーベル群の圏を ${\mathbf{Ab}}$ , ${\Gamma}$ 加群の圏を ${\mathbf{Mod}(\Gamma)}$ と書く．
定理 12.1. ${\mathbf{Mod}(\Gamma)\ni A\rightsquigarrow\mathrm{H}^{n}(\Gamma,A)\in\mathbf{Ab}}$ はコホモロジー ${\delta}$ 関手 (cohomological ${\delta}$ -functor):
1. ${0\rightarrow A\overset{f}{\rightarrow}B\overset{g}{\rightarrow}C\rightarrow0}$ ； ${\mathbf{Mod}(\Gamma)}$ の短完全列に対して， ${\exists \delta^{n}\in\mathrm{Hom}(\mathrm{H}^{n}(\Gamma,C),\mathrm{H}^{n+1}(\Gamma,A))}$ , ( ${n\in{\mathbb Z}_{\geq0}}$ ) s.t. 次は完全列:
  $\displaystyle 0 \longrightarrow A^{\Gamma}\overset{f}{\longrightarrow}B^{\Gamma}\overset{g}{\longrightarrow}C^{\Gamma}$
  
  $\displaystyle \overset{\delta^{0}}{\longrightarrow}\mathrm{H}^{1}(\Gamma,A)\overset{\mathrm{H}^{1}(\Gamma,f)}{\longrightarrow}\mathrm{H}^{1}(\Gamma,B)\overset{\mathrm{H}^{1}(\Gamma,g)}{\longrightarrow}\mathrm{H}^{1}(\Gamma,C)$
  
  $\displaystyle \overset{\delta^{1}}{\longrightarrow}\mathrm{H}^{2}(\Gamma,A)\overset{\mathrm{H}^{2}(\Gamma,f)}{\longrightarrow}\mathrm{H}^{2}(\Gamma,B)\overset{\mathrm{H}^{2}(\Gamma,g)}{\longrightarrow}\mathrm{H}^{2}(\Gamma,C)$
  
  $\displaystyle \overset{\delta^{2}}{\longrightarrow}\dots$
2. ${\mathbf{Mod}(\Gamma)}$ の各行が完全列である可換図式
  
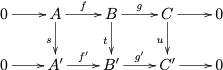
  に対して(i)の ${\delta^{n}}$ は次の可換図式を与える:
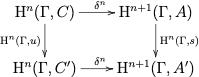
12.2. 余誘導加群
- ${\Delta\subset\Gamma}$ ；部分群， ${A\in\mathbf{Mod}(\Delta)}$ に対して，
  ${\mathrm{ind}_{\Delta}^{\Gamma}A}$ ； ${\mathrm{Hom}_{\Delta}({\mathbb Z}[\Gamma],A)}$ を ${\Gamma}$ 作用
  
  $\displaystyle \sigma(f)(\tau):=f(\tau\sigma),\quad\sigma,\,\tau\in\Gamma,\,f\in\mathrm{Hom}_{\Delta}({\mathbb Z}[\Gamma],A)$
  
  により ${\Gamma}$ 加群と見たもの（ ${A}$ の ${\Delta}$ から ${\Gamma}$ への余誘導加群 (coinduced module)）．
命題 12.1 (フロベニウス相互律). ${A\in\mathbf{Mod}(\Gamma)}$ , ${B\in\mathbf{Mod}(\Delta)}$ について自然な同型 ${\mathrm{Hom}_{\Gamma}(A,\mathrm{ind}_{\Delta}^{\Gamma}B) \cong \mathrm{Hom}_{\Delta}(A,B)}$ がある．

系 12.1 (シャピロの補題). ${\Delta\subset\Gamma}$ ；部分群． ${A\in\mathbf{Mod}(\Delta)}$ について自然な同型 ${\mathrm{H}^{n}(\Gamma,\mathrm{ind}_{\Delta}^{\Gamma}A)\cong\mathrm{H}^{n}(\Delta,A)}$ がある．

12.3. ガロアコホモロジー

定義 12.1. ${E/F}$ ；有限次ガロア拡大， ${A}$ ； ${\mathrm{Gal}(E/F)}$ 加群． ${n\in{\mathbb Z}_{\geq0}}$ に対して

$\displaystyle \mathrm{H}^{n}(E/F,A):=\mathrm{H}^{n}(\mathrm{Gal}(E/F),A)$

を ${A}$ 係数の ${n}$ 次ガロアコホモロジー群という．

系 12.2 (正規底定理). ${\mathrm{H}^{n}(E/F,E)=\{0\}}$ , ( ${n\in\mathbb{N}}$ )．

定理 12.2 (ヒルベルト 90 定理). ${\mathrm{H}^{1}(E/F,E^{\times})=\{1\}}$ .

1月7日低次方程式の解法

13.1. 巡回拡大
- ${n\in\mathbb{N}}$ ． ${F}$ ； ${1}$ の原始 ${n}$ 乗根 ${\zeta=\zeta_{n}}$ を含む体．
- ${1}$ の原始 ${n}$ 乗根の群
  $\displaystyle \mu_{n}=\mu_{n}(F):=\left\{ \zeta^{k}\mid k\in\mathbb{Z}/n\mathbb{Z}\right\} \simeq\mathbb{Z}/n\mathbb{Z}$
命題 13.1. ${\bar{a}}$ ； ${a\in F^{\times}}$ の ${F^{\times}/(F^{\times})^{n}}$ での像．
(i) ${\left\langle \bar{a}\right\rangle \simeq\mathbb{Z}/n\mathbb{Z}}$ のとき， ${E_{a}}$ ； ${x^{n}-a\in F[x]}$ の最小分解体， ${\alpha\in E_{a}}$ ； ${x^{n}-a}$ の根とすると，

$\displaystyle \partial\alpha:\mathrm{Gal}(E_{a}/F)\ni\sigma\longmapsto\sigma(\alpha)/\alpha\in\mu_{n}$

は ${\alpha}$ の取り方によらない同型．
(ii) ${\langle \bar{a}\rangle \mapsto E_{a}}$ は， ${F^{\times}/(F^{\times})^{n}}$ の ${n}$ 次巡回部分群の集合から， ${F}$ の ${n}$ 次巡回拡大の同型類の集合への全単射．

13.2. 三次方程式の解法
詳細略

13.3. 4次方程式の解法
詳細略

1月14日月曜日の授業を行う

1月21日ガロアの可解性定理
- 授業アンケート
- 期末試験の連絡
14.1. Galoisの可解性定理
- ；体．多項式, あるいは付随する方程式が冪根で解けるとは，その任意の解がの係数から
  - 四則演算と
  - ${n}$ 冪乗根, ( ${n\in\mathbb{N}}$ )を取る操作
  によって得られること．
- 群 ${G}$ の部分群 ${H}$ , ${K}$ の交換子群
  $\displaystyle [H,K]:=\left\langle hkh^{-1}k^{-1}\mid h\in H,\,k\in K\right\rangle.$
  
  ${H}$ , ${K}$ が正規部分群なら ${[H,K]}$ も正規部分群．
- ${G}$ の導来列
  $\displaystyle G=D^{0}(G)\triangleright D^{1}(G)\triangleright D^{2}(G)\triangleright\dots$
  
  を帰納的に ${D^{i}(G):=[D^{i-1}(G),D^{i-1}(G)]}$ , ( ${i\geq1}$ )で定める．
- が可解群であるとは，次の同値な2条件が成り立つこと．
  1. ある自然数 ${n}$ で ${D^{n}(G)=1}$ となる．
  2. 正規部分群の列 ${G=G^{0}\triangleright G^{1}\triangleright\dots\triangleright G^{n}=1}$ で各 ${G^{k}/G^{k+1}}$ , ( ${0\leq k<n}$ )がアーベル群になるものがある．
定理 14.1. ${F}$ ；標数 ${0}$ の体． ${f(x)\in F[x]}$ が根号で解けるためには，その最小分解体 ${E_{f}/F}$ のGalois群 ${\mathrm{Gal}(E_{f}/F)}$ が可解群であることが必要十分．

14.2. 代数閉包

定理 14.2 (シュタイニッツ (Steinitz)). (i)任意の体 ${F}$ の代数閉包が存在する．
(ii)代数拡大 ${E/F}$ と ${F}$ の代数閉包 ${\Omega}$ に対して， ${F}$ 代数の(単射)準同型 ${E\hookrightarrow\Omega}$ がある．さらに ${E}$ が代数閉体ならこれは同型になる．

注意 14.1. 上で ${E\hookrightarrow\Omega}$ は一意ではない．また自然な同型が存在するわけでもない．

1月28日出張のため休講

2月4日試験

成績評価について

代数学IIIの成績評価は期末テストの結果により行います．